题目内容
(2013•淄博二模)已知P(x,y)为函数y=1+lnx图象上一点,O为坐标原点,记直线OP的斜率k=f(x).
(I)若函数f(x)在区间(m,m+
)(m>0)上存在极值,求实数m的取值范围;
(II)当 x≥1时,不等式f(x)≥
恒成立,求实数t的取值范围;
(III)求证[(n+1)!]2>(n+1)•en-2(n∈N*).
(I)若函数f(x)在区间(m,m+
| 1 |
| 3 |
(II)当 x≥1时,不等式f(x)≥
| t |
| x+1 |
(III)求证[(n+1)!]2>(n+1)•en-2(n∈N*).
分析:(Ⅰ)由斜率公式求出k=f(x),求出导数f′(x),根据导数符号可判断f(x)的极值情况,要使函数f(x)在区间(m,m+
)(其中m>0)上存在极值,须有极值点在该区间内,从而得不等式组,解出即可;
(Ⅱ)由f(x)≥
得t≤
,令g(x)=
,则问题转化为求函数g(x)的最小值问题,利用导数研究函数g(x)的单调性,由单调性即可求得其最小值;
(Ⅲ)由(Ⅱ) 知f(x)≥
恒成立,即
≥
?lnx≥
=1-
>1-
,令x=n(n+1),则lnn(n+1)>1-
,
令n=1,2,3,…,n可得n个不等式,相加用裂项法化简后再变形即可得到结论;
| 1 |
| 3 |
(Ⅱ)由f(x)≥
| t |
| x+1 |
| (x+1)(1+lnx) |
| x |
| (x+1)(1+lnx) |
| x |
(Ⅲ)由(Ⅱ) 知f(x)≥
| 2 |
| x+1 |
| 1+lnx |
| x |
| 2 |
| x+1 |
| x-1 |
| x+1 |
| 2 |
| x+1 |
| 2 |
| x |
| 2 |
| n(n+1) |
令n=1,2,3,…,n可得n个不等式,相加用裂项法化简后再变形即可得到结论;
解答:解:(Ⅰ)由题意k=f(x)=
,x>0,
所以f′(x)=(
)′=-
,
当0<x<1时,f'(x)>0;当x>1时,f'(x)<0.
所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
故f(x)在x=1处取得极大值.
因为函数f(x)在区间(m,m+
)(其中m>0)上存在极值,
所以
,解得
<m<1.
故实数m的取值范围是(
,1).
(Ⅱ)由f(x)≥
得t≤
,
令g(x)=
,则g′(x)=
.
令h(x)=x-lnx,则h′(x)=1-
=
,
因为x≥1,所以h'(x)≥0,故h(x)在[1,+∞)上单调递增.
所以h(x)≥h(1)=1>0,从而g'(x)>0,g(x)在[1,+∞)上单调递增,g(x)≥g(1)=2,
所以实数t的取值范围是(-∞,2].
(Ⅲ)由(Ⅱ) 知f(x)≥
恒成立,
即
≥
?lnx≥
=1-
>1-
,
令x=n(n+1),则lnn(n+1)>1-
,
所以ln(1×2)>1-
,ln(2×3)>1-
,…,lnn(n+1)>1-
.
以上各式相加,ln[1×22×32×…×n2×(n+1)]>n-2[
+
+…+
]=n-2(1-
)>n-2,
所以1×22×32×…×n2×(n+1)>en-2,
所以[(n+1)!]2>(n+1)•en-2(n∈N*).
| 1+lnx |
| x |
所以f′(x)=(
| 1+lnx |
| x |
| lnx |
| x2 |
当0<x<1时,f'(x)>0;当x>1时,f'(x)<0.
所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
故f(x)在x=1处取得极大值.
因为函数f(x)在区间(m,m+
| 1 |
| 3 |
所以
|
| 2 |
| 3 |
故实数m的取值范围是(
| 2 |
| 3 |
(Ⅱ)由f(x)≥
| t |
| x+1 |
| (x+1)(1+lnx) |
| x |
令g(x)=
| (x+1)(1+lnx) |
| x |
| x-lnx |
| x2 |
令h(x)=x-lnx,则h′(x)=1-
| 1 |
| x |
| x-1 |
| x |
因为x≥1,所以h'(x)≥0,故h(x)在[1,+∞)上单调递增.
所以h(x)≥h(1)=1>0,从而g'(x)>0,g(x)在[1,+∞)上单调递增,g(x)≥g(1)=2,
所以实数t的取值范围是(-∞,2].
(Ⅲ)由(Ⅱ) 知f(x)≥
| 2 |
| x+1 |
即
| 1+lnx |
| x |
| 2 |
| x+1 |
| x-1 |
| x+1 |
| 2 |
| x+1 |
| 2 |
| x |
令x=n(n+1),则lnn(n+1)>1-
| 2 |
| n(n+1) |
所以ln(1×2)>1-
| 2 |
| 1×2 |
| 2 |
| 2×3 |
| 2 |
| n(n+1) |
以上各式相加,ln[1×22×32×…×n2×(n+1)]>n-2[
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| n(n+1) |
| 1 |
| n+1 |
所以1×22×32×…×n2×(n+1)>en-2,
所以[(n+1)!]2>(n+1)•en-2(n∈N*).
点评:本题考查利用导数研究函数的单调性、极值、最值,考查恒成立问题及不等式的证明,恒成立问题往往转化为求函数最值,解决本题(Ⅲ)问的关键是利用(Ⅱ)结论构造不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
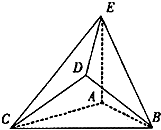 (2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
(2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD. (2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=
(2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=