Question

设全集为R，集合A={x||x-2|≤3}，B={x||y=lg（x-1）}，则C_B（A∩B）为

1. A.
   {x|1＜x≤5}
2. B.
   {x|x≤-1或x＞5}
3. C.
   {x|x≤1或x＞5}
4. D.
   {x|-1≤x≤5}

Answer 1

C
分析：集合A表示绝对值不等式的解集，集合B表示函数的定义域，化简集合A，B，然后借助数轴求出交集，最好根据补集的定义求出C_B（A∩B）即可．
解答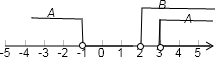：解：∵A={x||x-2|≤3}={x|-1≤x≤5}
B={x|y=lg（x-1）}={x|x-1＞0}={x|x＞1}
∴A∩B={x|1＜x≤5}
∴C_B（A∩B）={x|x≤1或x＞5}
故选C．
点评：本题考查解绝对值不等式、求函数的定义域、求集合的交集和补集，属于集合运算的基础题．