题目内容
已知两定点,坐标分别为A(-
,0),B(
,0),动点P满足条件∠PBA=2∠PAB,求动点P的轨迹C的方程.
| ||
| 3 |
2
| ||
| 3 |
分析:用动点P的坐标体现2∠PAB=∠PBA的最佳载体是直线PA、PB的斜率,确定直线的斜率可求.
解答:解:设P(x,y),∠PAB=α,则∠PBA=2α,它们是直线PA、PB的倾角还是倾角的补角,与点P在x轴的上方还是下方有关;以下讨论:
①若点P在x轴的上方,α∈(0,
),y>0,
此时,直线PA的倾角为α,PB的倾角为π-2α,
∴tanα=kPA=
,tan(π-2α)=
,(2α≠900)
∵tan(π-2α)=-tan2α,∴-
=
,得:3x2-y2=1,
∵|PA|≥|PB|,∴x≥
.
②当点P在x轴的下方时,y<0,同理可得点M的轨迹方程为3x2-y2=3(x≥
),
③当点P在线段AB上时,也满足2∠PAB=∠PBA,此时y=0,(-
<x<
).
综上所求点的轨迹方程为3x2-y2=1 (x≥
),y=0 (-
<x<
).
①若点P在x轴的上方,α∈(0,
| π |
| 2 |
此时,直线PA的倾角为α,PB的倾角为π-2α,
∴tanα=kPA=
| y | ||||
x+
|
| y | ||||
x-
|
∵tan(π-2α)=-tan2α,∴-
| y | ||||
x+
|
2×
| ||||||
1-(
|
∵|PA|≥|PB|,∴x≥
| ||
| 3 |
②当点P在x轴的下方时,y<0,同理可得点M的轨迹方程为3x2-y2=3(x≥
| ||
| 3 |
③当点P在线段AB上时,也满足2∠PAB=∠PBA,此时y=0,(-
| ||
| 3 |
2
| ||
| 3 |
综上所求点的轨迹方程为3x2-y2=1 (x≥
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
点评:本题考查轨迹方程,考查学生的计算能力,如何体现动点M满足的条件2∠PAB=∠PBA是解决本题的关键,属于中档题.

练习册系列答案
相关题目
 已知两定点M,N的坐标分别为(-6,0),(6,0),动点P与M,N的连线斜率之积为
已知两定点M,N的坐标分别为(-6,0),(6,0),动点P与M,N的连线斜率之积为 已知两定点M,N的坐标分别为(-6,0),(6,0),动点P与M,N的连线斜率之积为
已知两定点M,N的坐标分别为(-6,0),(6,0),动点P与M,N的连线斜率之积为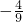 ,求动点P的轨迹方程,并画出轨迹草图.
,求动点P的轨迹方程,并画出轨迹草图.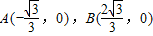 ,动点P满足条件∠PBA=2∠PAB,求动点P的轨迹C的方程.
,动点P满足条件∠PBA=2∠PAB,求动点P的轨迹C的方程.