题目内容
(文科)已知平面向量
=(2,-2),
=(3,4),
•
=
•
,则|
|的最小值是( )
| a |
| b |
| a |
| b |
| a |
| c |
| c |
分析:设
=(x,y),由
•
=
•
,可得y=x+1,代入|
|=
=
=
,利用二次函数的性质可求最小值
| c |
| a |
| b |
| a |
| c |
| c |
| x2+y2 |
| x2+(x+1)2 |
| 2x2+2x+1 |
解答:解:设
=(x,y),
∵
•
=
•
,
•
=2×3+(-2)×4=-2,
•
=2x-2y
∴2x-2y=-2
∴y-x=1
∵|
|=
=
=
=
≥
故当x=-
时,|
|最小值为
故选D
| c |
∵
| a |
| b |
| a |
| c |
| a |
| b |
| a |
| c |
∴2x-2y=-2
∴y-x=1
∵|
| c |
| x2+y2 |
| x2+(x+1)2 |
| 2x2+2x+1 |
=
2(x+
|
| ||
| 2 |
故当x=-
| 1 |
| 2 |
| c |
| ||
| 2 |
故选D
点评:本题主要考查了向量的数量积的坐标表示,利用配方求解二次函数的最值,属于基础试题

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
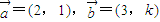 ,若
,若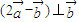 ,则实数k= .
,则实数k= .