题目内容
已知函数![]()
(I)求函数![]() 上的最大值及最小值;
上的最大值及最小值;
(II)对![]() ,如果函数
,如果函数![]() 的图象在函数
的图象在函数![]() 的图象的下方,则称函数
的图象的下方,则称函数![]() 在区 间D上被函数
在区 间D上被函数![]() 覆盖。求证:函数
覆盖。求证:函数![]() 上被函数
上被函数![]() 覆盖。
覆盖。
解:(Ⅰ)由已知![]()
所以函数![]() 上单调递增。
上单调递增。
所以函数![]() 上的最大、最小值分别为
上的最大、最小值分别为![]()
因为 ![]()
所以函数![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为 ![]()
(Ⅱ)设![]()
因为![]() ,所以函数
,所以函数![]() 上单调递减。
上单调递减。
又 ![]() ,所以,在区间
,所以,在区间![]() 上,
上,![]()
所以函数![]() 的图象在函数
的图象在函数 ![]() 图象的下方,
图象的下方,
所以函数被![]() 覆盖。
覆盖。

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目

 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.
 成立,求实数a的取值范围;
成立,求实数a的取值范围;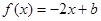 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.