题目内容
已知z是复数,z+3i、
均为实数(i为虚数单位),
(1)求复数z;
(2)求一个以z为根的实系数一元二次方程.
| z | 3-i |
(1)求复数z;
(2)求一个以z为根的实系数一元二次方程.
分析:(1)设z=x+yi(x、y∈R),根据z+3i、
均为实数可求出x与y的值,从而求出所求;
(2)若实系数一元二次方程有虚根z=9-3i,则必有共轭虚根
=9+3i,求出z+
与z•
根据根与系数的关系可得一个以z为根的实系数一元二次方程.
| z |
| 3-i |
(2)若实系数一元二次方程有虚根z=9-3i,则必有共轭虚根
. |
| z |
. |
| z |
. |
| z |
解答:解:(1)设z=x+yi(x、y∈R),
z+3i=x+(y+3)i,由题意得 y=-3.…(3分)
=
=
(3x+3)+
(x-9)i
由题意得x=9.∴z=9-3i.…(7分)
(2)若实系数一元二次方程有虚根z=9-3i,则必有共轭虚根
=9+3i.…(10分)
z+
=18,z•
=90,…(12分)
∴所求的一个一元二次方程可以是x2-18x+90=0.…(14分)
z+3i=x+(y+3)i,由题意得 y=-3.…(3分)
| z |
| 3-i |
| x-3i |
| 3-i |
| 1 |
| 10 |
| 1 |
| 10 |
由题意得x=9.∴z=9-3i.…(7分)
(2)若实系数一元二次方程有虚根z=9-3i,则必有共轭虚根
. |
| z |
z+
. |
| z |
. |
| z |
∴所求的一个一元二次方程可以是x2-18x+90=0.…(14分)
点评:本题主要考查了复数代数形式的乘除运算,以及根与系数的关系,同时考查了共轭复数等基本概念,属于基础题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
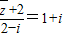 ,则z等于( )
,则z等于( )