题目内容
选做题:矩阵与变换在平面直角坐标系xOy中,直线x+y+2=0在矩阵M=
|
分析:在直线x+y+2=0上取两点A(-2,0),B(0,-2),A,B在矩阵M对应的变换作业下分别对应于点A',B',分别求出点A',B'的坐标,代入直线m,建立方程组,解之即可.
解答:解:在直线x+y+2=0上取两点A(-2,0),B(0,-2)
A,B在矩阵M对应的变换作业下分别对应于点A',B'
因为
=
,所以A'的坐标为(-2,-2b);
=
,所以B'的坐标为(-2a,-8);
由题意可知A',B'在直线m:x-y-4=0上,所以
解得:a=2,b=3
A,B在矩阵M对应的变换作业下分别对应于点A',B'
因为
|
|
|
|
|
|
由题意可知A',B'在直线m:x-y-4=0上,所以
|
解得:a=2,b=3
点评:本题主要考查了几种特殊的矩阵变换,同时考查了计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
从A,B,C,D四个中选做2个,每题10分,共20分
| A.选修4—1 几何证明选讲 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:  。 。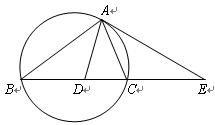 |
| B.选修4—2 矩阵与变换 在平面直角坐标系 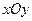 中,设椭圆 中,设椭圆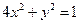 在矩阵对应的变换作用下得到曲线F,求F的方程。 在矩阵对应的变换作用下得到曲线F,求F的方程。 |
| C.选修4—4 参数方程与极坐标 在平面直角坐标系 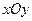 中,点 中,点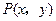 是椭圆 是椭圆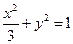 上的一个动点,求 上的一个动点,求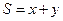 的最大值。 的最大值。 |
| D.选修4—5 不等式证明选讲 |
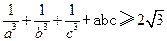 。
。  (2012•江苏一模)选做题
(2012•江苏一模)选做题 (2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,
(2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答, 对应的变换作用下得直线m:x-y-4=0,求实数a,b的值.
对应的变换作用下得直线m:x-y-4=0,求实数a,b的值.