题目内容
已知函数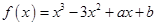 在
在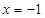 处的切线与
处的切线与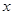 轴平行.
轴平行.
(1)求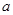 的值和函数
的值和函数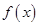 的单调区间;
的单调区间;
(2)若函数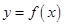 的图象与抛物线
的图象与抛物线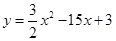 恰有三个不同交点,求
恰有三个不同交点,求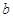 的取值范围.
的取值范围.
【答案】
(1) ;函数
;函数 的单调递增区间为
的单调递增区间为 ;
; 的单调递减区间为
的单调递减区间为 ;(2)
;(2) 的取值范围
的取值范围 .
.
【解析】
试题分析:(1)首先求函数 的导数,由已知条件函数
的导数,由已知条件函数 在
在 处的切线与
处的切线与 轴平行,解方程
轴平行,解方程 可得
可得 的值;解不等式
的值;解不等式 可得函数
可得函数 的单调递增区间,解不等式
的单调递增区间,解不等式 可得函数
可得函数 的单调递减区间为;(2) 令
的单调递减区间为;(2) 令 ,则由题意等价于
,则由题意等价于 有三个不同的根,即
有三个不同的根,即 的极小值为小于0,且
的极小值为小于0,且 的极大值为大于0.因此利用导数求函数
的极大值为大于0.因此利用导数求函数 的极大极小值,列不等式组并求解即得
的极大极小值,列不等式组并求解即得 的取值范围.
的取值范围.
试题解析:(1)  ,
(2分)
,
(2分)
由 ,解得
,解得 .
(3分)
.
(3分)
则 ,
,
故 的单调递增区间为
的单调递增区间为 ;
; 的单调递减区间为
的单调递减区间为 .
.
(判断过程给两分) (7分)
(2)令 , (8分)
, (8分)
则原题意等价于 有三个不同的根.
有三个不同的根.
∵ ,
(9分)
,
(9分)
∴ 在
在 上递增,在
上递增,在 上递减. (10分)
上递减. (10分)
则 的极小值为
的极小值为 ,且
,且 的极大值为
的极大值为 ,
,
解得 .
.  的取值范围
的取值范围 .
(13分)
.
(13分)
考点:1.导数的几何意义;2.利用导数求函数的单调区间、极值;3.利用导数求参数的值.

练习册系列答案
相关题目
 (
( ).
). 在
在 处的切线与x轴平行,求a的值,并求出函数的极值;
处的切线与x轴平行,求a的值,并求出函数的极值; ,在(1)的条件下,若
,在(1)的条件下,若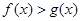 恒成立,求b的取值范围.
恒成立,求b的取值范围. (
( ).
). 在
在 处的切线与x轴平行,求a的值,并求出函数的极值;
处的切线与x轴平行,求a的值,并求出函数的极值; ,在(1)的条件下,若
,在(1)的条件下,若 恒成立,求b的取值范围.
恒成立,求b的取值范围.