题目内容
正方体ABCED-A1B1C1D1中,E、F分别为AB、AD的中点,则AD1与EF所成角是
- A.45°
- B.30°
- C.60°
- D.90°
C
分析:在正方体中建立空间直角坐标系,给两条异面直线赋予向量意义,求出两个向量的坐标,求出两个向量的数量积及两个向量的模,求出两个向量的夹角,进一步求出两异面直线的夹角.
解答:以D为坐标原点,分别以DA,DC,DD1为x,y,z轴建立空间直角坐标系,不妨设正方体的棱长为1则有
A(1,0,0),D1(0,0,1),
∴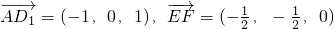
∴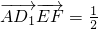
∵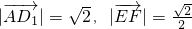
∴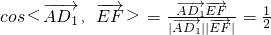
∴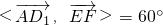
故选C.
点评:求两异面直线的夹角常利用的工具是向量,先将异面直线赋予向量意义,再利用向量的数量积公式求出两个向量的夹角,根据异面直线与相应的向量的夹角的关系求出两异面直线的夹角.
分析:在正方体中建立空间直角坐标系,给两条异面直线赋予向量意义,求出两个向量的坐标,求出两个向量的数量积及两个向量的模,求出两个向量的夹角,进一步求出两异面直线的夹角.
解答:以D为坐标原点,分别以DA,DC,DD1为x,y,z轴建立空间直角坐标系,不妨设正方体的棱长为1则有
A(1,0,0),D1(0,0,1),

∴
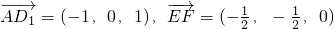
∴
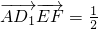
∵
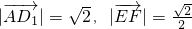
∴
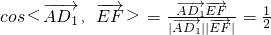
∴
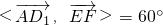
故选C.
点评:求两异面直线的夹角常利用的工具是向量,先将异面直线赋予向量意义,再利用向量的数量积公式求出两个向量的夹角,根据异面直线与相应的向量的夹角的关系求出两异面直线的夹角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
正方体ABCED-A1B1C1D1中,E、F分别为AB、AD的中点,则AD1与EF所成角是( )
| A、45° | B、30° | C、60° | D、90° |