题目内容
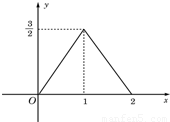
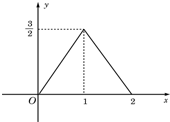 如图所示的图象所表示的函数解析式为
如图所示的图象所表示的函数解析式为f(x)=
|
f(x)=
.
|
分析:分段求解:分别把0≤x≤1及1≤x≤2时的解析式求出即可.
解答:解:当0≤x≤1时,设f(x)=kx,由图象过点(1,
),得k=
,所以此时f(x)=
x;
当1≤x≤2时,设f(x)=mx+n,由图象过点(1,
),(2,0),得
,解得
,所以此时f(x)=-
x+3.
故答案为:f(x)=
.
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
当1≤x≤2时,设f(x)=mx+n,由图象过点(1,
| 3 |
| 2 |
|
|
| 3 |
| 2 |
故答案为:f(x)=
|
点评:本题考查函数解析式的求解问题,本题根据图象可知该函数为分段函数,分两段用待定系数法求得.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间t(分)的函数关系表示的图象只可能是( )
如图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间t(分)的函数关系表示的图象只可能是( ) 如图所示的图象所表示的函数解析式为________.
如图所示的图象所表示的函数解析式为________.