题目内容
矩形ABCD的长AB=8,宽AD=5,动点E、F分别在边BC、CD上,且CE=CF=x,将△AEF的面积S表示为x的函数f(x).
(1)求函数S=f(x)的解析式及定义域;
(2)求S的值域.
(1)求函数S=f(x)的解析式及定义域;
(2)求S的值域.
分析:(1)利用几何图形的关系,欲求△AEF的面积S,利用平行四边形的面积减去三个三角形的面积计算即得,最后结合实际问题写出定义域.
(2)利用(1)中得出的二次函数f(x)在x∈(0,5]上单调性,即可求得函数S的值域.
(2)利用(1)中得出的二次函数f(x)在x∈(0,5]上单调性,即可求得函数S的值域.
解答:解:(1)S=f(x)=S平行四边形ABCD-S△CEF-S△ABE-S△ADF
=40-
x2-
×8×(5-x)-
×5×(8-x)
=-
x2+
x
=-
(x-
)2+
.
∵CE≤CB≤CD,∴0<x≤5,
∴函数S=f(x)的解析式:S=f(x)=-
(x-
)2+
(0<x≤5);
定义域(0,5];
(2)∵f(x)在x∈(0,5]上单调递增,∴Smax=f(5)=20,
即S的最大值为20.
∴值域(0,20].
=40-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 13 |
| 2 |
=-
| 1 |
| 2 |
| 13 |
| 2 |
| 169 |
| 8 |
∵CE≤CB≤CD,∴0<x≤5,
∴函数S=f(x)的解析式:S=f(x)=-
| 1 |
| 2 |
| 13 |
| 2 |
| 169 |
| 8 |
定义域(0,5];
(2)∵f(x)在x∈(0,5]上单调递增,∴Smax=f(5)=20,
即S的最大值为20.
∴值域(0,20].
点评:本小题主要考查函数模型的选择与应用、二次函数的最值问题,属于基础题.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
 如图,矩形ABCD的长AB=2,宽AD=x,若PA⊥平面ABCD,矩形的边CD上至少有一个点Q,使得PQ⊥BQ,则x的范围是( )
如图,矩形ABCD的长AB=2,宽AD=x,若PA⊥平面ABCD,矩形的边CD上至少有一个点Q,使得PQ⊥BQ,则x的范围是( )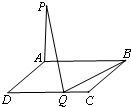 如图,矩形ABCD的长AB=2,宽AD=x,若PA⊥平面ABCD,矩形的边CD上至少有一个点Q,使得PQ⊥BQ,则x的范围是
如图,矩形ABCD的长AB=2,宽AD=x,若PA⊥平面ABCD,矩形的边CD上至少有一个点Q,使得PQ⊥BQ,则x的范围是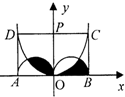 如图,矩形ABCD的长AB=6cm,宽AD=3cm.O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线y=ax2经过C、D两点,则图中阴影部分的面积是
如图,矩形ABCD的长AB=6cm,宽AD=3cm.O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线y=ax2经过C、D两点,则图中阴影部分的面积是