题目内容
(本小题满分12分)
|
(1)求p的值;
(2)过该抛物线的焦点作两条互相垂直的直线l1,l2,与抛物线相交得两条弦,两条弦
的中点分别为G,H.求|GH|的最小值.
解:(Ⅰ)设![]() ,
,
因为抛物线的焦点![]() ,
,
则![]() .……………………………1分
.……………………………1分
![]() ,………2分
,………2分
![]() ,而点A在抛物线上,
,而点A在抛物线上,
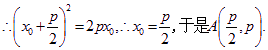 .……………………………………4分
.……………………………………4分
又![]() 故所求抛物线的方程为
故所求抛物线的方程为![]() .6分
.6分
(2)由![]() ,得
,得![]() ,显然直线
,显然直线![]() ,
,![]() 的斜率都存在且都不为0.
的斜率都存在且都不为0.
设![]() 的方程为
的方程为![]() ,则
,则![]() 的方程为
的方程为![]() .
.
由 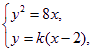 得
得![]() ,同理可得
,同理可得![]() .……………8分
.……………8分
则![]()
=![]()
![]() .(当且仅当
.(当且仅当![]() 时取等号)
时取等号)
所以![]() 的最小值是8.……………………………………12分
的最小值是8.……………………………………12分
解析:
同答案

练习册系列答案
相关题目