题目内容
(本小题满分12分)
在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.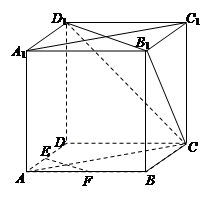
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1
(1)连结BD,
 ,
, EF∥平面CB1D(2)AA1⊥平面A1B1C1D1,
EF∥平面CB1D(2)AA1⊥平面A1B1C1D1, AA1⊥B1D1,又A1C1⊥B1D1
AA1⊥B1D1,又A1C1⊥B1D1 B1D1⊥平面CAA1C1
B1D1⊥平面CAA1C1 平面CAA1C1⊥平面CB1D1
平面CAA1C1⊥平面CB1D1
解析试题分析:(1)证明:连结BD.
在长方体 中,对角线
中,对角线 .
.
又 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点, .
. .
.
又B1D1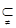 平面
平面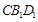 ,
,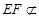 平面
平面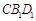 ,
,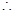 EF∥平面CB1D1.
EF∥平面CB1D1.
(2)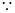 在长方体
在长方体 中,AA1⊥平面A1B1C1D1,而B1D1
中,AA1⊥平面A1B1C1D1,而B1D1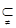 平面A1B1C1D1,
平面A1B1C1D1,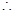 AA1⊥B1D1.
AA1⊥B1D1.
又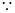 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1,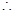 B1D1⊥平面CAA1C1.
B1D1⊥平面CAA1C1.
又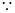 B1D1
B1D1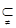 平面CB1D1,
平面CB1D1,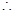 平面CAA1C1⊥平面CB1D1.
平面CAA1C1⊥平面CB1D1.
考点:线面平行垂直的判定
点评:线面平行的判定:需在平面内找一直线与面外直线平行,本题充分借助出现的中点可考虑中位线的平行关系;面面垂直的判定:要证两面垂直需在其中一个平面内找到另外一面的垂线,即将证明面面垂直问题转化为证明线面垂直

练习册系列答案
相关题目
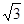 .
.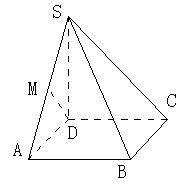
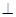 SC;
SC; 的底面
的底面 是等腰梯形,
是等腰梯形, 且
且


 分别是
分别是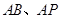 的中点.
的中点.
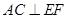 ;
; 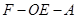 的余弦值.
的余弦值.
 AD=1,CD=
AD=1,CD=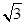 .
.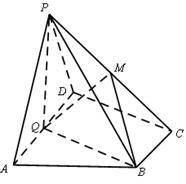
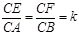 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). 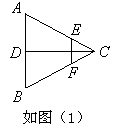
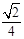 ,求k的值.
,求k的值. 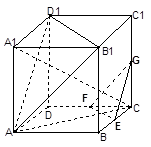
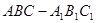 中, AC=4,CB=2,AA1=2,
中, AC=4,CB=2,AA1=2,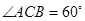 ,E、F分别是
,E、F分别是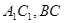 的中点。
的中点。
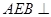 平面
平面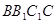 ;
;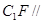 平面ABE;
平面ABE;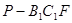 的体积。
的体积。 中,
中,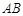 ∥
∥ ,
, ,
, ,
, ⊥
⊥ ,
, ⊥
⊥ 为
为 的中点.
的中点.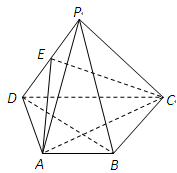
 ∥平面
∥平面 ;
; .
.