题目内容
（1）化简：
+log2
（2）计算：tan70°cos10°（
tan20°-1）
| (log25)2-4log25+4 |
| 1 |
| 5 |
（2）计算：tan70°cos10°（
| 3 |
分析：（1）利用平方差公式与对数的运算性质即可求得
+log2
的值；
（2）将已知关系式中的“切”化“弦”，再利用三角函数的恒等变换化简求值即可．
| (log25)2-4log25+4 |
| 1 |
| 5 |
（2）将已知关系式中的“切”化“弦”，再利用三角函数的恒等变换化简求值即可．
解答：解：（1）∵
=log25-2，
∴原式=log25-2+log2
=-2+log2(5×
)=-2+log21=-2；
（2）原式=
•
=
•
=-
=-
=-2．
| (log25)2-4log25+4 |
∴原式=log25-2+log2
| 1 |
| 5 |
| 1 |
| 5 |
（2）原式=
| sin70°cos10° |
| cos70° |
| ||
| cos20° |
=
| sin70°cos10° |
| cos70° |
| 2sin(20°-30°) |
| cos20° |
=-
| 2sin70°sin20° |
| cos70°cos20° |
=-
| 2sin70°sin20° |
| sin20°sin70° |
=-2．
点评：本题考查对数的运算性质与三角函数的恒等变换及化简求值，属于中档题．
练习册系列答案
相关题目
化简结果为
；（2）log（x+1）（x+1）=1成立的条件是x≠-1；（3）
与
的大小关系是
；（4）
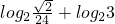的值为
．
+
-
；
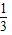
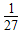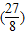
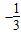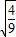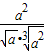（a＞0）．
化简结果为
；（2）log（x+1）（x+1）=1成立的条件是x≠-1；（3）
与
的大小关系是
；（4）
的值为
．