��Ŀ����
���������жϣ�
��1��b=0�Ǻ���f��x��=ax2+bx+cΪż�����ij�Ҫ������
��2����Բ
+
=1�У��Ե㣨1��1��Ϊ�е��������ֱ�߷���Ϊx+2y-3=0��
��3���ع�ֱ��
=
x+
�ع���(
��
)��
��4����ͼ����������ABCD�У���EΪ��BCD�����ģ���
=
+
+
��
��5��˫����
-
=1(a��0��b��0)��������ΪF1��F2��PΪ��֧�������Ҷ������һ�㣬��PF1F2������ԲԲ��ΪT�����T�ĺ�����Ϊa��������ȷ����������______��

��1��b=0�Ǻ���f��x��=ax2+bx+cΪż�����ij�Ҫ������
��2����Բ
| x2 |
| 4 |
| y2 |
| 3 |
��3���ع�ֱ��
 |
| y |
 |
| b |
 |
| a |
| . |
| x |
| . |
| y |
��4����ͼ����������ABCD�У���EΪ��BCD�����ģ���
| AE |
| AB |
| 1 |
| 2 |
| AC |
| 2 |
| 3 |
| AD |
��5��˫����
| x2 |
| a2 |
| y2 |
| b2 |

��1������f��x��=ax2+bx+c��ż�������ɵ�f��-x��=f��x������a��-x��2-bx+c=ax2+bx+c����-bx=bx����b=0����b=0ʱ��f��x��=ax2+c������f��-x��=f��x������ż����������b=0�Ǻ���f��x��=ax2+bx+cΪż�����ij�Ҫ�������ʣ�1����ȷ��
��2������A��1��1��Ϊ�е���Բ��������Բ����E��x1��y1����F��x2��y2������A��1��1��ΪEF�е㣬��x1+x2=2��y1+y2=2����E��x1��y1����F��x2��y2���ֱ������Բ
+
=1����
����3��x1+x2����x1-x2��+4��y1+y2����y1-y2��=0����6��x1-x2��+8��y1-y2��=0����k=
=-
������A��1��1��Ϊ�е���Բ�������ڵ�ֱ�߷���Ϊ3x+4y-7=0���ʣ�2������
��3���ع�ֱ��
=
x+
�ع���(
��
)������ȷ��
��4����������ABCD�У���EΪ��BCD�����ģ���
=
+
=
+
•
(
+
)=
(
+
+
)���ʣ�4������ȷ��
��5�����PF1F2������Բ�ֱ���PF1��PF2���ڵ�A��B����F1F2���ڵ�M����|PA|=|PB|��|F1A|=|F1M|��|F2B|=|F2M|���ֵ�P��˫������֧�ϣ���|PF1|-|PF2|=2a������|PA|+|F1A|��-��|PB|+|F2B|��=2a����|F1M|-|F2M|=2a����|F1M|+|F2M|=2c����M������Ϊ��x��0������|F1M|-|F2M|=2a���ࣨx+c��-��c-x��=2a�����x=a���ʣ�5����ȷ��
�ʴ�Ϊ����1����3����5����
��2������A��1��1��Ϊ�е���Բ��������Բ����E��x1��y1����F��x2��y2������A��1��1��ΪEF�е㣬��x1+x2=2��y1+y2=2����E��x1��y1����F��x2��y2���ֱ������Բ
| x2 |
| 4 |
| y2 |
| 3 |
|
| y1-y2 |
| x1-x2 |
| 3 |
| 4 |
��3���ع�ֱ��
 |
| y |
 |
| b |
 |
| a |
| . |
| x |
| . |
| y |
��4����������ABCD�У���EΪ��BCD�����ģ���
| AE |
| AB |
| BE |
| AB |
| 2 |
| 3 |
| 1 |
| 2 |
| BC |
| BD |
| 1 |
| 3 |
| AB |
| AC |
| AD |
��5�����PF1F2������Բ�ֱ���PF1��PF2���ڵ�A��B����F1F2���ڵ�M����|PA|=|PB|��|F1A|=|F1M|��|F2B|=|F2M|���ֵ�P��˫������֧�ϣ���|PF1|-|PF2|=2a������|PA|+|F1A|��-��|PB|+|F2B|��=2a����|F1M|-|F2M|=2a����|F1M|+|F2M|=2c����M������Ϊ��x��0������|F1M|-|F2M|=2a���ࣨx+c��-��c-x��=2a�����x=a���ʣ�5����ȷ��
�ʴ�Ϊ����1����3����5����

��ϰ��ϵ�д�
�����Ŀ

 �ض����� �� ��
�ض����� �� ��
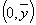
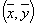
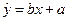 �ع�����________.
�ع�����________.