题目内容
(1)设函数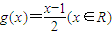 ,且数列{cn}满足c1=1,cn=g(cn-1)(n∈N,n>1);求数列{cn}的通项公式.
,且数列{cn}满足c1=1,cn=g(cn-1)(n∈N,n>1);求数列{cn}的通项公式.(2)设等差数列{an}、{bn}的前n项和分别为Sn和Tn,且
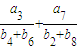 =
=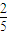 ,
,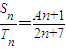 ,S2=6;求常数A的值及{an}的通项公式.
,S2=6;求常数A的值及{an}的通项公式.(3)若
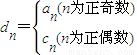 ,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.
,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.
【答案】分析:(1)先求出数列{cn}的递推公式,再对递推公式进性构造新数列,利用新数列的通项公式,求数列{cn}的通项公式.
(2)先利用等差数列的性质求出: ,再对
,再对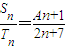 变形求出常数A的值;再把所求的A的值代入
变形求出常数A的值;再把所求的A的值代入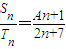 和S2=6;相结合求出数列{an}的前n项和分别为Sn和就可求出{an}的通项公式.
和S2=6;相结合求出数列{an}的前n项和分别为Sn和就可求出{an}的通项公式.
(3)把(1)、(2)中求出的数列{an}、{cn}的通项公式代入;再分n为奇数和偶数两种情况分别求和即可.
解答:解:(1)由题意: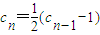 ,
,
变形得: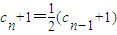 ,(1分)
,(1分)
∴数列{cn+1}是以 为公比,c1+1=2为首项的等比数列.(3分)
为公比,c1+1=2为首项的等比数列.(3分)
∴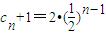 ,
,
即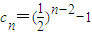 .(5分)
.(5分)
(2)∵由等差数列{an}、{bn}知:b4+b6=b2+b8=2b5,a3+a7=2a5;
∴由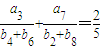 得:
得: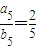 ,(6分)
,(6分)
∴ ,
,
∵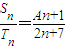 ,
,
∴ ,解得A=1;
,解得A=1;
(8分)
∴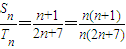 ,Sn和Tn分别是等差数列{an}、{bn}的前n项和;
,Sn和Tn分别是等差数列{an}、{bn}的前n项和;
∴可设Sn=kn(n+1),Tn=kn(2n+7);
∵S2=6,
∴k=1,即Sn=n2+n.(10分)
当n=1时,a1=S1=2,
当n≥2时,an=Sn-Sn-1=n2+n-[(n-1)2+(n-1)]=2n.
综上得:an=2n.(12分)
(3)当n=2k+1(k∈N*)时,d1+d2+…+dn=(a1+a3++a2k+1)+(c2+c4++c2k)
=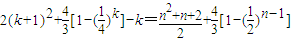 (14分)
(14分)
当n=2k(k∈N*)时,d1+d2++dn=(a1+a3++a2k-1)+(c2+c4++c2k)
=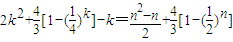 .(16分)
.(16分)
点评:本题涉及了等差数列的求和公式以及等比数列求和公式的应用.在对等比数列求和时,一定要清楚公比的取值,再代入公式.
(2)先利用等差数列的性质求出:
 ,再对
,再对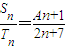 变形求出常数A的值;再把所求的A的值代入
变形求出常数A的值;再把所求的A的值代入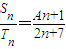 和S2=6;相结合求出数列{an}的前n项和分别为Sn和就可求出{an}的通项公式.
和S2=6;相结合求出数列{an}的前n项和分别为Sn和就可求出{an}的通项公式.(3)把(1)、(2)中求出的数列{an}、{cn}的通项公式代入;再分n为奇数和偶数两种情况分别求和即可.
解答:解:(1)由题意:
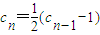 ,
,变形得:
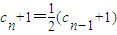 ,(1分)
,(1分)∴数列{cn+1}是以
 为公比,c1+1=2为首项的等比数列.(3分)
为公比,c1+1=2为首项的等比数列.(3分)∴
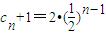 ,
,即
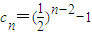 .(5分)
.(5分)(2)∵由等差数列{an}、{bn}知:b4+b6=b2+b8=2b5,a3+a7=2a5;
∴由
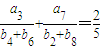 得:
得: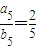 ,(6分)
,(6分)∴
 ,
,∵
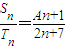 ,
,∴
 ,解得A=1;
,解得A=1;(8分)
∴
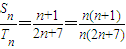 ,Sn和Tn分别是等差数列{an}、{bn}的前n项和;
,Sn和Tn分别是等差数列{an}、{bn}的前n项和;∴可设Sn=kn(n+1),Tn=kn(2n+7);
∵S2=6,
∴k=1,即Sn=n2+n.(10分)
当n=1时,a1=S1=2,
当n≥2时,an=Sn-Sn-1=n2+n-[(n-1)2+(n-1)]=2n.
综上得:an=2n.(12分)
(3)当n=2k+1(k∈N*)时,d1+d2+…+dn=(a1+a3++a2k+1)+(c2+c4++c2k)
=
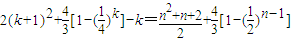 (14分)
(14分)当n=2k(k∈N*)时,d1+d2++dn=(a1+a3++a2k-1)+(c2+c4++c2k)
=
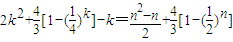 .(16分)
.(16分)点评:本题涉及了等差数列的求和公式以及等比数列求和公式的应用.在对等比数列求和时,一定要清楚公比的取值,再代入公式.

练习册系列答案
相关题目
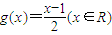 ,且数列{cn}满足c1=1,cn=g(cn-1)(n∈N,n>1);求数列{cn}的通项公式.
,且数列{cn}满足c1=1,cn=g(cn-1)(n∈N,n>1);求数列{cn}的通项公式.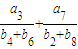 =
=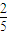 ,
,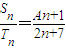 ,S2=6;求常数A的值及{an}的通项公式.
,S2=6;求常数A的值及{an}的通项公式.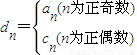 ,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.
,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.