题目内容
椭圆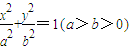 的离心率
的离心率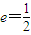 ,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)与圆x2+y2=2的位置关系是 .
,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)与圆x2+y2=2的位置关系是 .
【答案】分析:由题设知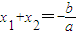 ,
,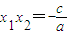 ,x12+x22=(x1+x2)2-2x1x2=
,x12+x22=(x1+x2)2-2x1x2=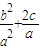 =
=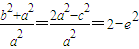 .由此可知点P(x1,x2)与圆x2+y2=2的位置关系.
.由此可知点P(x1,x2)与圆x2+y2=2的位置关系.
解答:解:∵离心率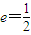 ,∴a=2c.
,∴a=2c.
∵方程ax2+bx-c=0的两个根分别为x1,x2,
∴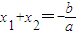 ,
,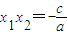 ,
,
∴x12+x22=(x1+x2)2-2x1x2
=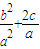 =
=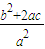
=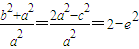 <2.
<2.
∴点P(x1,x2)在圆x2+y2=2内.
故答案为:点在圆内.
点评:本题考查圆锥曲线的性质和应用,解题时要要认真审题,仔细解答.
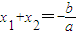 ,
,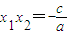 ,x12+x22=(x1+x2)2-2x1x2=
,x12+x22=(x1+x2)2-2x1x2=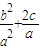 =
=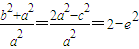 .由此可知点P(x1,x2)与圆x2+y2=2的位置关系.
.由此可知点P(x1,x2)与圆x2+y2=2的位置关系.解答:解:∵离心率
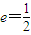 ,∴a=2c.
,∴a=2c.∵方程ax2+bx-c=0的两个根分别为x1,x2,
∴
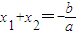 ,
,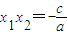 ,
,∴x12+x22=(x1+x2)2-2x1x2
=
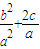 =
=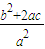
=
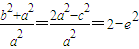 <2.
<2.∴点P(x1,x2)在圆x2+y2=2内.
故答案为:点在圆内.
点评:本题考查圆锥曲线的性质和应用,解题时要要认真审题,仔细解答.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
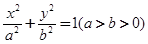 的离心率
的离心率 ,右焦点到直线
,右焦点到直线 的距离为
的距离为 ,过
,过 的直线
的直线 交椭圆于
交椭圆于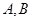 两点.(Ⅰ) 求椭圆的方程;(Ⅱ)
若直线
两点.(Ⅰ) 求椭圆的方程;(Ⅱ)
若直线 轴于
轴于 ,
,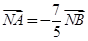 ,求直线
,求直线 的离心率
的离心率 ,右焦点到直线
,右焦点到直线 的距离
的距离
 为坐标原点。
为坐标原点。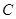 的方程;
的方程; 两点,证明点
两点,证明点 的距离为定值,并求弦
的距离为定值,并求弦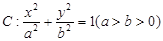 的离心率
的离心率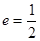 ,右焦点到直线
,右焦点到直线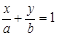 的距离
的距离
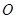 为坐标原点。
为坐标原点。 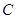 的方程;
的方程;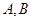 两点,证明点
两点,证明点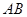 的距离为定值,并求弦
的距离为定值,并求弦
 的离心率
的离心率 ,右焦点到直线
,右焦点到直线 的距离
的距离
 为坐标原点.
为坐标原点. 的方程;
的方程; 两点,证明点
两点,证明点 的距离为定值,并求弦
的距离为定值,并求弦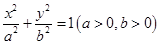 的离心率
的离心率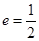 ,右焦点
,右焦点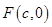 ,方程
,方程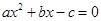 的两个根分别为
的两个根分别为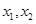 ,则点
,则点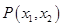 在
在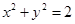 内 B.圆
内 B.圆