题目内容
如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
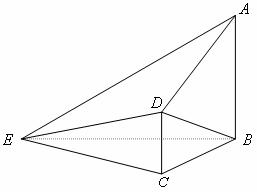
【命题意图】本题考查空间位置关系、二面角等有关知识,考查空间想象能力,中等题.
【答案】(Ⅰ)证明:取BE的中点O,AE的中点F,连OC,OF,DF,则2OF![]() BA
BA
∵AB⊥平面BCE,CD⊥平面BCE,∴2CD ![]() BA,
BA,
∴OF![]() CD,∴OC∥FD
CD,∴OC∥FD
∵BC=CE,∴OC⊥BE,又AB⊥平面BCE.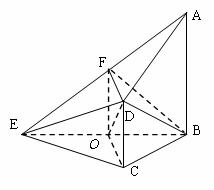
∴OC⊥平面ABE. ∴FD⊥平面ABE.
从而平面ADE⊥平面ABE. ………………6分
(Ⅱ)二面角A—EB—D与二面角F—EB—D相等,
由(Ⅰ)知二面角F—EB—D的平面角为∠FOD。
BC=CE=2, ∠BCE=1200,OC⊥BE得BO=OE=![]() ,OC=1,
,OC=1,
∴OFDC为正方形,∴∠FOD=![]() ,
,
∴二面角A—EB—D的大小为![]() . ……………………12分
. ……………………12分
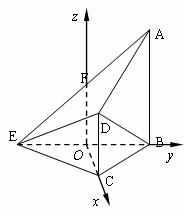
解法2:取BE的中点O,连OC.∵BC=CE, ∴OC⊥BE,又AB⊥平面BCE.
以O为原点建立如图空间直角坐标系O-xyz,
则由已知条件有: ![]() ,
,![]() ,
,![]()
![]()
![]()
设平面ADE的法向量为![]() ,
,
则由![]() ·
·![]()
![]()
![]()
![]()
及![]() ·
·![]()
![]()
![]()
![]()
可取![]()
![]()
![]()
又AB⊥平面BCE,∴AB⊥OC,OC⊥平面ABE,
∴平面ABE的法向量可取为![]() =
=![]() .
.
∵![]() ·
·![]()
![]()
![]() ·
·![]() =0, ∴
=0, ∴![]() ⊥
⊥![]() ,∴平面ADE⊥平面ABE.…… 6分
,∴平面ADE⊥平面ABE.…… 6分
(Ⅱ)设平面BDE的法向量为![]() ,
,
则由![]() ·
·![]()
![]()
![]()
![]()
及![]() ·
·![]()
![]()
![]()
![]() 可取
可取![]()
![]()
![]()
∵平面ABE的法向量可取为![]() =
=![]()
∴锐二面角A—EB—D的余弦值为![]() =
=![]() ,
,
∴二面角A—EB—D的大小为![]() . ……………………………12分
. ……………………………12分

练习册系列答案
相关题目
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.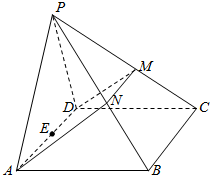 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点. 如图,在四棱锥
如图,在四棱锥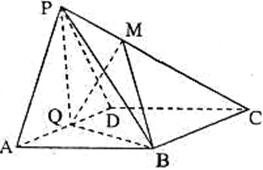 试确定
试确定