题目内容

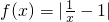已知函数 $数学公式$ ，其中x∈（o，+∞）．
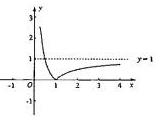
（I）在给定的坐标系中，画出函数f（x）的图象；
（II）设0＜a＜b，且f（a）=f（b），证明：ab＞1．

证明：（I）不等式可以变为f（x）= $\text{[math]}$
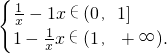
对函数进行分析知f（x）在（0，1]上是减函数，在（1，+∞）上是增函数．
其图象为：
（II）：由题意f（a）=f（b）?|1- $\text{[math]}$ |=|1- $\text{[math]}$ |?（1- $\text{[math]}$ ）²=（1- $\text{[math]}$ ）²?2ab=a+b≥2 $\text{[math]}$
故ab- $\text{[math]}$ ≥0，即 $\text{[math]}$ （ $\text{[math]}$ -1）≥0，
故 $\text{[math]}$ -1≥0，故ab＞1．
分析：（I）去绝对值号将函数变为分段函数，即f（x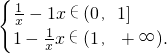）= $\text{[math]}$ 分段作出图象即可；
（II）当0＜a＜b，且f（a）=f（b）时，由f（a）=f（b）?|1- $\text{[math]}$ |=|1- $\text{[math]}$ |?（1- $\text{[math]}$ ）²=（1- $\text{[math]}$ ）²?2ab=a+b≥2 $\text{[math]}$ 得到关于ab的不等式，解出不等式的解集，由解集确定ab＞1．
点评：本题考点是函数的图象、绝对值不等式的解法，考查利用绝对值不等式这一工具证明不等式，二者的结合点相当隐蔽，本题需要对题设条件进行转化证明，请注意体会这里的技巧．

练习册系列答案

金状元绩优好卷系列答案

快乐考卷系列答案

全程领航系列答案

全国重点高中提前招生同步强化训练卷系列答案

无敌卷王系列答案

培优100分系列小学总复习小升初必备系列答案

专题讲练3年中考2年模拟系列答案

一飞冲天初中总复习中考专项系列答案

名校调研跟踪测试卷系列答案

好成绩1加1学习导航系列答案

相关题目

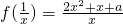已知函数 $数学公式$ ，其中x∈（0，1]
（Ⅰ）当a= $数学公式$ 时，求f（x）的最小值；
（Ⅱ）在定义域内，f（x）＞0恒成立，试求实数a的取值范围．

（本小题满分13分）已知函数（其中x≥1且x≠2）．

（1）求函数的反函数

（2）设，求函数最小值及相应的x值；

（3）若不等式对于区间上的每一个x值都成立，求实数m的取值范围.

（其中x∈R，A＞0，ω＞0）的图象与x轴的交点中，相邻两个交点之间的距离为

，且图象上一个点为

．
（1）求f（x）的解析式；
（2）已知m∈R，p：关于x的不等式f（x）≥m²+2m-2对

恒成立；q：函数y=（m²-1）^x是增函数．若“p或q”为真，“p且q”为假，求实数m的取值范围．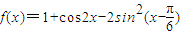

，其中x∈R，则下列结论中正确的是（）
A．f（x）是最小正周期为π的偶函数
B．f（x）的一条对称轴是

C．f（x）的最大值为2
D．将函数

的图象左移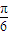

得到函数f（x）的图象

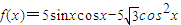（其中x∈R）．
求：
①函数f（x）的最小正周期；
②函数f（x）的单调递减区间；
③函数f（x）图象的对称轴．