题目内容
已知A(x1,f(x1)),B(x2,f(x2))是函数f(x)=2sin(wx+j)(w>0, <j<0)图象上的任意两点,且角j的终边经过点P(l,-
<j<0)图象上的任意两点,且角j的终边经过点P(l,- ),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为
),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为 .
.
(1)求函数f(x)的解析式;(2)求函数f(x)的单调递增区间;(3)当x∈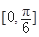 时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
(1)f(x)=2sin(3x- );(2)[
);(2)[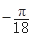 +
+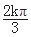 ,
,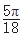 +
+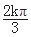 ], k∈Z;(3)[
], k∈Z;(3)[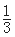 ,+¥).
,+¥).
解析试题分析:(1)由角j的终边经过点P(l,- )及
)及 <j<0可求得j的值,又|f(x1)-f(x2)|=4时,|x1-x2|的最小值为
<j<0可求得j的值,又|f(x1)-f(x2)|=4时,|x1-x2|的最小值为 可最小正周期为
可最小正周期为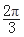 ,从而可求出w的值,即可求出其表达式;(2)由复合函数的知识可令3x-
,从而可求出w的值,即可求出其表达式;(2)由复合函数的知识可令3x- =u,只需令
=u,只需令 +2kp≤u≤
+2kp≤u≤ +2kp,解出x的范围即是函数的单调递增区间;(3)不等式mf(x)+2m≥f(x)恒成立要求m的范围,只需用分离变量的作法,等价于
+2kp,解出x的范围即是函数的单调递增区间;(3)不等式mf(x)+2m≥f(x)恒成立要求m的范围,只需用分离变量的作法,等价于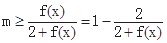 ,而x∈
,而x∈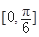 ,可求出f(x)的范围,从而可求出
,可求出f(x)的范围,从而可求出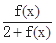 的最大值,则m恒大于或等于其最大值.
的最大值,则m恒大于或等于其最大值.
试题解析:(1)角j的终边经过点P(1,- ),tanj=-
),tanj=- ,∵
,∵ <j<0,∴j=-
<j<0,∴j=- .由|f(x1)-f(x2)|=4时,|x1-x2|的最小值为
.由|f(x1)-f(x2)|=4时,|x1-x2|的最小值为 ,得T=
,得T=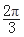 ,即
,即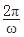 =
=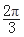 ,∴w=3,∴f(x)=2sin(3x-
,∴w=3,∴f(x)=2sin(3x- )
)
(2)令 +2kp≤3x-
+2kp≤3x- ≤
≤ +2kp,得
+2kp,得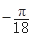 +
+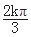 ≤x≤
≤x≤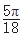 +
+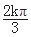 ,k∈Z
,k∈Z
∴函数f(x)的单调递增区间为[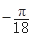 +
+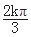 ,
,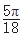 +
+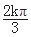 ],k∈Z.
],k∈Z.
(3)当x∈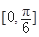 时,-
时,- ≤f(x)≤1,所以2+f(x)>0,mf(x)+2m≥f(x)等价于
≤f(x)≤1,所以2+f(x)>0,mf(x)+2m≥f(x)等价于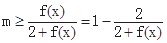 .由-
.由- ≤f(x)≤1,得
≤f(x)≤1,得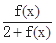 的最大值为
的最大值为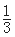 ,所以实数m的取值范围是[
,所以实数m的取值范围是[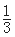 ,+¥).
,+¥).
考点:三角函数的定义,三角函数的周期公式,正弦函数的单调区间,恒成立问题,分离变量法,转化思想.

练习册系列答案
相关题目

 取得最大值时,求自变量
取得最大值时,求自变量 的集合;
的集合; 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到? 在一个周期内,当
在一个周期内,当 时,
时, 取得最小值
取得最小值 ;当
;当 时,
时,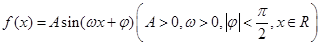 图象的一部分如图所示.
图象的一部分如图所示. 的解析式;
的解析式; 时,求函数
时,求函数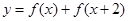 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.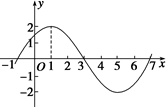
 ;
; 的周期和单调递增区间;
的周期和单调递增区间; 在
在 上有解,求实数m的取值范围.
上有解,求实数m的取值范围. ,且
,且 ∥
∥ .
. ;
;  .
.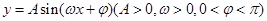 ,
,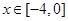 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,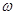 和
和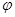 的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设
的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设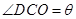 (弧度),试用
(弧度),试用 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)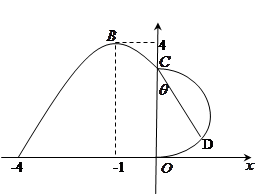
 .
. ,求
,求 的取值构成的集合.
的取值构成的集合. ,求
,求 的值.
的值. ;
;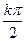 ,k∈Z};
,k∈Z}; )的图象向右平移
)的图象向右平移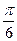 个单位得到y=3sin2x的图象;
个单位得到y=3sin2x的图象;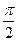 )在[0,
)在[0,