题目内容
定义g(x)表示如下函数:若m-
<x≤m+
(m∈Z),则g(x)=m.给出下列关于函数f(x)=|x-g(x)|的四个命题:
(1)函数y=f(x)的定义域是R,值域是[0,
];
(2)函数y=f(x)是R上的奇函数;
(3)函数y=f(x)是周期函数,最小正周期是1;
(4)函数y=f(x)的图象关于直线x=
(k∈Z)对称.
其中正确命题的序号是
| 1 |
| 2 |
| 1 |
| 2 |
(1)函数y=f(x)的定义域是R,值域是[0,
| 1 |
| 2 |
(2)函数y=f(x)是R上的奇函数;
(3)函数y=f(x)是周期函数,最小正周期是1;
(4)函数y=f(x)的图象关于直线x=
| k |
| 2 |
其中正确命题的序号是
(1)(3)(4)
(1)(3)(4)
.(把你认为正确的命题序号都填上)分析:由已知若m-
<x≤m+
(m∈Z),则g(x)=m,因为m为整数,故可取m为几个特殊的整数,画出函数的图象进行研究即可得到正确结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答: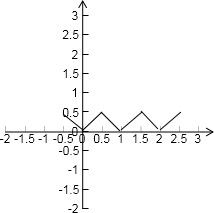 解:由题意x-g(x)=x-m,f(x)=|x-g(x)|=|x-m|,
解:由题意x-g(x)=x-m,f(x)=|x-g(x)|=|x-m|,
m=0时,-
<x≤
,f(x)=|x|,
m=1时,1-
<x≤1+
,f(x)=|x-1|,
m=2时,2-
<x≤2+
,f(x)=|x-2|,
由图象可知:
(1)y=f(x)的定义域为R,值域为[0,
],正确;
(2)函数y=f(x)是R上的偶函数,故不正确;
(3)y=f(x)是周期函数,最小正周期为1,正确;
(4)y=f(x)的图象关于直线x=
(k∈Z)对称,正确;
故答案为:(1)(3)(4)
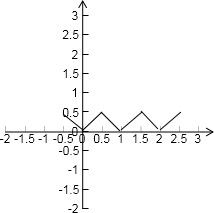 解:由题意x-g(x)=x-m,f(x)=|x-g(x)|=|x-m|,
解:由题意x-g(x)=x-m,f(x)=|x-g(x)|=|x-m|,m=0时,-
| 1 |
| 2 |
| 1 |
| 2 |
m=1时,1-
| 1 |
| 2 |
| 1 |
| 2 |
m=2时,2-
| 1 |
| 2 |
| 1 |
| 2 |
由图象可知:
(1)y=f(x)的定义域为R,值域为[0,
| 1 |
| 2 |
(2)函数y=f(x)是R上的偶函数,故不正确;
(3)y=f(x)是周期函数,最小正周期为1,正确;
(4)y=f(x)的图象关于直线x=
| k |
| 2 |
故答案为:(1)(3)(4)
点评:本题主要考查了函数单调性的判断与证明,以及周期性、对称性、奇偶性等性质,也是一个新定义问题,可结合图象进行研究,体现数形结合思想,属于中档题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目

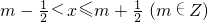 ,则g(x)=m.给出下列关于函数f(x)=|x-g(x)|的四个命题:
,则g(x)=m.给出下列关于函数f(x)=|x-g(x)|的四个命题: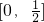 ;
;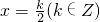 对称.
对称.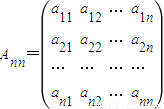 ,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设
,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设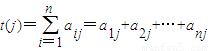 .
.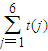 ;
;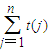 =
=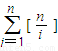 ;
;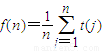 ,
,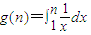 ,求证:g(n)-1<f(n)<g(n)+1.
,求证:g(n)-1<f(n)<g(n)+1. ,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设
,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设 .
. ;
; =
= ;
; ,
, ,求证:g(n)-1<f(n)<g(n)+1.
,求证:g(n)-1<f(n)<g(n)+1.