题目内容
(12分)若二次函数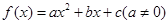 满足
满足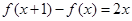 ,且
,且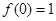 .(1)求
.(1)求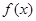 的解析式;(2)若在区间
的解析式;(2)若在区间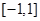 上,不等式
上,不等式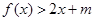 恒成立,求实数
恒成立,求实数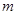 的取值范围.
的取值范围.
【答案】
(1)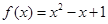 ;(2)
;(2)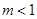
【解析】(1)先根据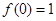 ,得:
,得: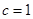 ,然后再根据
,然后再根据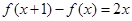 化简整理后可得
化简整理后可得
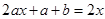 ,从而可得a=1,b=-1.进而得到
,从而可得a=1,b=-1.进而得到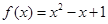 .
.
(2)原不等式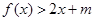 可化简为
可化简为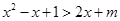 ,即:
,即: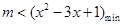 ,
,
然后令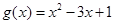 求其在工间[-1,1]上的最小值即可.
求其在工间[-1,1]上的最小值即可.
(1)有题可知: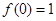 ,解得:
,解得: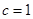
由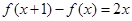 .可知:
.可知: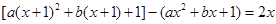
化简得: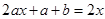
所以: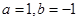 .∴
.∴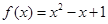
(2)不等式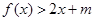 可化简为
可化简为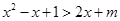
即: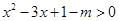
设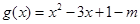 ,则其对称轴为
,则其对称轴为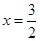 ,∴
,∴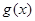 在[-1,1]上是单调递减函数.
在[-1,1]上是单调递减函数.
因此只需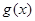 的最小值大于零即可,∴
的最小值大于零即可,∴
代入得: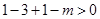 解得:
解得: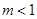
所以实数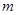 的取值范围是:
的取值范围是: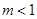

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
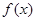 满足
满足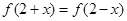 ,且
,且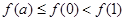 ,则实数
,则实数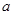 的取值范围是_________.
的取值范围是_________.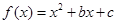 满足
满足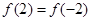 ,且函数的
,且函数的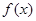 的一个零点为
的一个零点为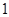 .
.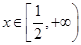 ,
,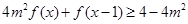 恒成立,求实数
恒成立,求实数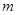 的取值范围.
的取值范围.