Question

已知椭圆C的两个焦点是(0，-)和(0，)，并且经过点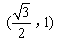，抛物线E的顶点在坐标原点，焦点F恰好是椭圆C的右顶点．

（Ⅰ）求椭圆C和抛物线E的标准方程；

（Ⅱ）过点F作两条斜率都存在且互相垂直的直线l1、l2，l1交抛物线E于点A、B，l2交抛物线E于点G、H，求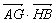的最小值．

 

Answer 1

【答案】

（I）椭圆C的标准方程为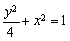；抛物线E的标准方程为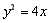；（Ⅱ）最小值为16．

【解析】

试题分析：（I）由题意得c=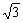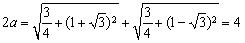，，从而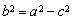=1，椭圆C的标准方程为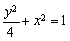．该椭圆右顶点的坐标为(1，0)，即抛物线的焦点为(1，0)，所以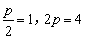，抛物线E的标准方程为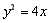．（Ⅱ）设l1的方程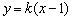：，l2的方程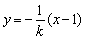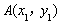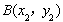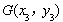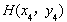，，，，.注意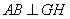，且它们交于点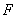，所以可将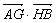作如下变形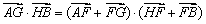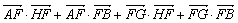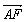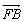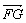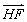： ==||·||+||·||，这样先将|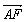|·||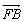+||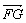·||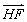用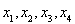表示出来，再利用韦达定理用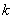表示，从而求得其最小值.

试题解析：（I）设椭圆的标准方程为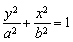(a>b>0)，焦距为2c，

则由题意得c=，，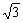

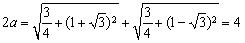∴a=2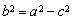，=1，

∴椭圆C的标准方程为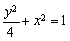． 4分

∴右顶点F的坐标为(1，0)．

设抛物线E的标准方程为，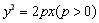

∴，

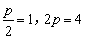∴抛物线E的标准方程为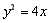． 6分

（Ⅱ）设l1的方程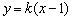：，l2的方程，

，，，，

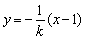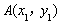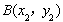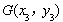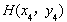由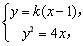 消去y得：，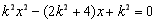

∴ x1+x2=2+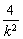，x1x2=1．

由消去y得：x2-(4k2+2)x+1=0，

∴x3+x4=4k2+2，x3x4=1， 9分

∴

=

=||·||+||·||

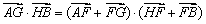
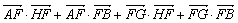
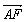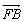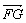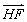=|x1+1|·|x2+1|+|x3+1|·|x4+1|

=(x1x2+x1+x2+1)+(x3x4+x3+x4+1)

=8+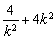

≥8+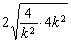

=16．

当且仅当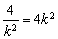即k=±1时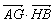，有最小值16． 13分

考点：1、椭圆与抛物线；2、直线与圆锥曲线.