题目内容
某厂生产产品x件的总成本c(x)=1200+| 2 |
| 75 |
| k |
| x |
分析:利用100件产品单价50万求出常量k,确定出p关于x的解析式,利润=单价-成本.总利润l(x)=p-c.求出l的导数,令导数=0时,函数有最值求出可得.
解答:解:由题意知有:502=
,解得:k=25×104,
∴P=
=
;
∴总利润L(x)=x•
-1200-
x3=500
-1200-
x3,
∴L′(x)=250x-
-
x2;
令L′(x)=0则有:x=25(件)
∴当x=25件时,总利润最大.
| k |
| 100 |
∴P=
|
| 500 | ||
|
∴总利润L(x)=x•
| 500 | ||
|
| 2 |
| 75 |
| x |
| 2 |
| 75 |
∴L′(x)=250x-
| 1 |
| 2 |
| 2 |
| 25 |
令L′(x)=0则有:x=25(件)
∴当x=25件时,总利润最大.
点评:考查学生利用导数求闭区间上函数的最值.

练习册系列答案
相关题目
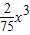 (万元),已知产品单价P(万元)与产品件数x满足:P2=
(万元),已知产品单价P(万元)与产品件数x满足:P2=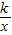 ,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?
,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?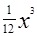 (万元),已知产品单价P(万元) 与产品件数x满足:
(万元),已知产品单价P(万元) 与产品件数x满足: ,生产1件这样的产品单价为16万元.
,生产1件这样的产品单价为16万元.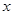 件时,总利润为
件时,总利润为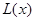 (万元),求
(万元),求