题目内容
已知向量 =(
=( sin
sin ,1),
,1), =(cos
=(cos ,cos2
,cos2 )
)
(1)若 ·
· =1,求cos(
=1,求cos( -x)的值;
-x)的值;
(2)记f(x)= ·
· ,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
【答案】
(1)-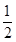 .(2)
(1,
.(2)
(1,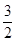 ).
).
【解析】
试题分析:(1)∵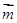 ·
·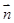 =1,即
=1,即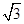 sin
sin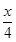 cos
cos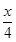 +cos2
+cos2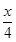 =1,
=1,
即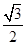 sin
sin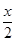 +
+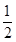 cos
cos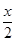 +
+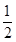 =1,
=1,
∴sin(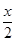 +
+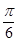 )=
)=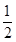 .
.
∴cos(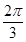 -x)=cos(x-
-x)=cos(x-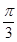 )=-cos(x+
)=-cos(x+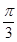 )=-[1-2sin2(
)=-[1-2sin2(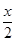 +
+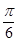 )]
)]
=2·(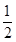 )2-1=-
)2-1=-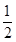 .
.
(2)∵(2a-c)cosB=bcosC,
由正弦定理得(2sinA-sinC)cosB=sinBcosC.
∴2sinAcosB-cosBsinC=sinBcosC,
∴2sinAcosB=sin(B+C),
∵A+B+C=π,∴sin(B+C)=sinA,且sinA≠0,
∴cosB=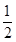 ,B=
,B=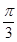 ,∴0<A<
,∴0<A<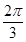 .
.
∴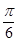 <
< +
+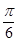 <
<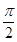
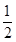 <sin(
<sin( +
+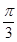 )<1.
)<1.
又∵f(x)=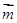 ·
·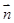 =sin(
=sin(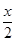 +
+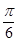 )+
)+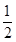 ,
,
∴f(A)=sin(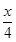 +
+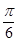 )+
)+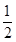 .
.
故函数f(A)的取值范围是(1,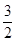 ).
).
考点:本题综合考查了向量、三角函数及正余弦定理
点评:三角与向量是近几年高考的热门题型,这类题往往是先进行向量运算,再进行三角变换

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 =(sin
=(sin ,1),
,1), =(1,cos
=(1,cos .
. =(sin
=(sin ,1),
,1), =(1,cos
=(1,cos .
.