题目内容
已知椭圆C: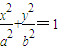 (a>b>0)的一个焦点到长轴的两个端点的距离分别为2+
(a>b>0)的一个焦点到长轴的两个端点的距离分别为2+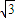 和2-
和2-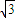 .
.(1)求椭圆的方程;
(2)设过定点M(0,2)的直线l与椭圆C交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
(3)如图,过原点O任意作两条互相垂直的直线与椭圆
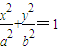 (a>b>0)交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.
(a>b>0)交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.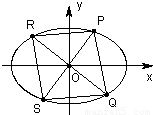
【答案】分析:(1)由椭圆的几何性质可得焦点到长轴的两个端点的距离分别为a+c和a-c,再把所给数值代入即可.
(2)斜率k的取值范围,须将k用其它参数表示,先设直线l的方程,代入椭圆方程,求x1+x2和x1x2,再根据∠AOB为锐角得到向量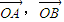 的数量积大于0,用直线l的斜率k表示
的数量积大于0,用直线l的斜率k表示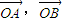 的数量积,即可得到k的范围.
的数量积,即可得到k的范围.
(3)先根据椭圆的对称性判断PQSR是菱形,原点O到各边的距离相等.设四边形PQSR的一条对角线的方程,根据菱形对角线互相垂直,可得另一条对角线的方程,分别与椭圆方程联立,再借助菱形各边长相等,即可得到a,b满足的条件.
解答:解:(1)由题意得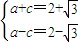 ,解得a=2,c=
,解得a=2,c=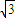 ,b=1
,b=1
所求的方程为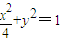
(2)显然直线x=0不满足题设条件,可设直线l:y=kx+2,A(x1,y1)
由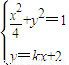 得(1+4k2)x2+16kx+12=0.
得(1+4k2)x2+16kx+12=0.
∵△=(16k)2-4×12(1+4k2)>0,∴k∈(-∞,-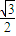 )∪(
)∪(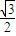 ,+∞)(1)
,+∞)(1)
又x1+x2= ,
,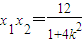
由0°<∠AOE<90°?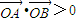 ∴
∴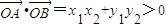
所以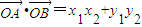 =x1x2+(kx1+2)(kx2+2)
=x1x2+(kx1+2)(kx2+2)
=(1+k2)x1x2+2k(x1+x2)+4=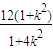 +2k
+2k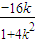 +4>0
+4>0
∴-2<k<2 (2)
由(1)(2)得:k∈(-2,-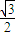 )∪(
)∪(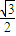 ,2).
,2).
(3)由椭圆的对称性可知PQSR是菱形,原点O到各边的距离相等.
当P在y轴上,Q在x轴上时,直线PQ的方程为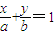 ,由d=1得
,由d=1得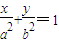 ,
,
当P不在y轴上时,设直线PS的斜率为k,P(x1,kx1),则直线RQ的斜率为-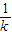 ,Q(x2,-
,Q(x2,-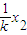 )
)
由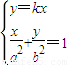 ,得
,得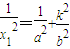 (1),同理
(1),同理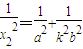 (2)
(2)
在Rt△OPQ中,由 d|PQ|=
d|PQ|= |OP||OQ|,即|PQ|2=|OP|2•|OQ|2
|OP||OQ|,即|PQ|2=|OP|2•|OQ|2
所以 ,化简得
,化简得 ,
,
k2(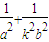 )+
)+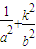 =1+k2,即
=1+k2,即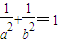 .
.
综上,d=1时a,b满足条件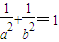
点评:本体考查了椭圆性质的应用,以及判断直线与椭圆位置关系时,韦达定理的应用.
(2)斜率k的取值范围,须将k用其它参数表示,先设直线l的方程,代入椭圆方程,求x1+x2和x1x2,再根据∠AOB为锐角得到向量
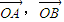 的数量积大于0,用直线l的斜率k表示
的数量积大于0,用直线l的斜率k表示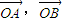 的数量积,即可得到k的范围.
的数量积,即可得到k的范围.(3)先根据椭圆的对称性判断PQSR是菱形,原点O到各边的距离相等.设四边形PQSR的一条对角线的方程,根据菱形对角线互相垂直,可得另一条对角线的方程,分别与椭圆方程联立,再借助菱形各边长相等,即可得到a,b满足的条件.
解答:解:(1)由题意得
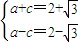 ,解得a=2,c=
,解得a=2,c=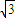 ,b=1
,b=1所求的方程为
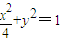
(2)显然直线x=0不满足题设条件,可设直线l:y=kx+2,A(x1,y1)
由
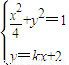 得(1+4k2)x2+16kx+12=0.
得(1+4k2)x2+16kx+12=0.∵△=(16k)2-4×12(1+4k2)>0,∴k∈(-∞,-
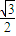 )∪(
)∪(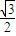 ,+∞)(1)
,+∞)(1)又x1+x2=
 ,
,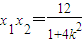
由0°<∠AOE<90°?
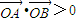 ∴
∴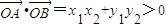
所以
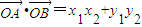 =x1x2+(kx1+2)(kx2+2)
=x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+2k(x1+x2)+4=
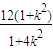 +2k
+2k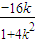 +4>0
+4>0∴-2<k<2 (2)
由(1)(2)得:k∈(-2,-
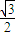 )∪(
)∪(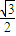 ,2).
,2).(3)由椭圆的对称性可知PQSR是菱形,原点O到各边的距离相等.
当P在y轴上,Q在x轴上时,直线PQ的方程为
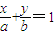 ,由d=1得
,由d=1得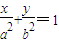 ,
,当P不在y轴上时,设直线PS的斜率为k,P(x1,kx1),则直线RQ的斜率为-
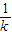 ,Q(x2,-
,Q(x2,-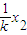 )
)由
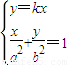 ,得
,得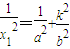 (1),同理
(1),同理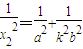 (2)
(2)在Rt△OPQ中,由
 d|PQ|=
d|PQ|= |OP||OQ|,即|PQ|2=|OP|2•|OQ|2
|OP||OQ|,即|PQ|2=|OP|2•|OQ|2所以
 ,化简得
,化简得 ,
,k2(
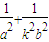 )+
)+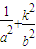 =1+k2,即
=1+k2,即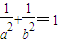 .
.综上,d=1时a,b满足条件
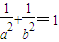
点评:本体考查了椭圆性质的应用,以及判断直线与椭圆位置关系时,韦达定理的应用.

练习册系列答案
相关题目
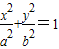 (a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为
(a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为 .
. (O为坐标原点),求△AOB的面积;
(O为坐标原点),求△AOB的面积;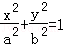 (a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点
(a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点 .
. ,求点Q的轨迹方程.
,求点Q的轨迹方程. (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为 ,直线y=k(x-1)与椭圆C交于不同的两点M、N.
,直线y=k(x-1)与椭圆C交于不同的两点M、N. 时,求k的值.
时,求k的值. +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C(
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C( ,0)求实数k的取值范围。
,0)求实数k的取值范围。 (a>b>0)的离心率为
(a>b>0)的离心率为 ,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若 。则
。则 ( )
( )  (D)
(D)