题目内容
如图,点D为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,DM⊥BB1交AA1与点M,DN⊥BB1交CC1于点N.
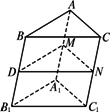
(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:
DE2=DF2+EF2-2DF·EFcos∠DFE,拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并加以证明.
答案:
解析:
解析:
|
证明:(1)∵CC1∥BB1,∴CC1⊥DM,CC1⊥DN ∴CC1⊥面DMN,从而CC1⊥MN. (2)在斜三棱柱ABC-A1B1C1中,则 其中α是侧面AA1B1B与侧面CC1B1B成的二面角的平面角. 在△DMN中,MN2=DM2+DN2-2DM·DNcosα 两边同时乘以侧棱长平方即BB12,便有结论成立. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



