Question

根据定义在集合A上的函数y=f（x），构造一个数列发生器，其工作原理如下：①输入数据x∈A，计算出x=f（x）；②若x₁∉A，则数列发生器结束工作；若x₁∈A，则输出x₁，并将x₁反馈回输入端，再计算出x₂=f（x₁），依次规律继续下去．若集合A={x|0＜x＜1}，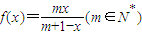
（Ⅰ）求证：x∈A时，f（x）∈A．
（Ⅱ）求证：对任意x∈A，此数列发生器都可以产生一个无穷数列去{x_n}
（Ⅲ）若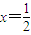，记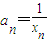（n∈N^*），求数列{a_n}的通项公式．

Answer 1

【答案】分析：（Ⅰ）当x∈A，即0＜x＜1时，由m∈N^*，知m+1-x＞0．所以，由，能够证明f（x）∈A．
（Ⅱ）由（Ⅰ）知，对任意x∈A，有x₁=f（x）∈A，由x₁∈A，可得x₂=f（x₁）∈A，由x₂∈A，可得x₃=f（x₂）∈A，
依此规律继续下去，此数列发生器都可以产生一个无穷数列{x_n}．
（Ⅲ）由，得．所以，因为，所以{a_n-1}是首项为，公比为的等比数列．由此能求出数列{a_n}的通项公式．
解答：（Ⅰ）证明：当x∈A，即0＜x＜1时，
∵m∈N^*，
∴m+1-x＞0．
∴，
∵，
∴，
∴f（x）∈A．
（Ⅱ）证明：由（Ⅰ）知，对任意x∈A，有x₁=f（x）∈A，
由x₁∈A，可得x₂=f（x₁）∈A，
由x₂∈A，可得x₃=f（x₂）∈A，
依此规律继续下去，此数列发生器都可以产生一个无穷数列{x_n}．
（Ⅲ）解：由，
可得．
∴，
即，
∵，
∴{a_n-1}是首项为，公比为的等比数列．
∴，
∴．
点评：本题首先考查数列与函数的综合运用，对数学思维的要求比较高，有一定的探索性．综合性强，难度大，易出错．解题时要认真审题，仔细解答，注意构造法的合理运用．