题目内容
(本小题14分)设函数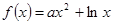 .
.
(Ⅰ)讨论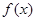 的单调性;
的单调性;
(Ⅱ)已知 ,若函数
,若函数 的图象总在直线
的图象总在直线 的下方,求
的下方,求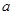 的取值范围;
的取值范围;
(Ⅲ)记 为函数
为函数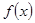 的导函数.若
的导函数.若 ,试问:在区间
,试问:在区间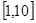 上是否存在
上是否存在 (
(
 )个正数
)个正数 …
…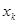 ,使得
,使得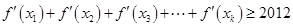 成立?请证明你的结论.
成立?请证明你的结论.
【答案】
(1)当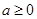 时,
时,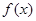 的递增区间是
的递增区间是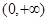 ;当
;当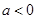 时,
时,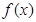 在
在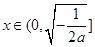 上单调递增;在
上单调递增;在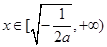 上单调递减
上单调递减
(2)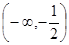 (3)存在,证明见解析
(3)存在,证明见解析
【解析】
试题分析:
(Ⅰ)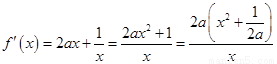 ,
,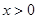 ……2分
……2分
①当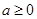 时,
时,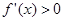 恒成立,故
恒成立,故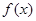 的递增区间是
的递增区间是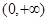 ; ……3分
; ……3分
②当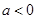 时,令
时,令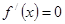 ,则
,则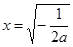 .
.
当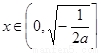 时,
时,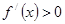 ;当
;当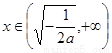 时,
时,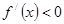 .
.
故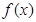 在
在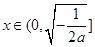 上单调递增;在
上单调递增;在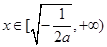 上单调递减;
……6分
上单调递减;
……6分
(Ⅱ)由上述讨论,当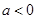 时,
时,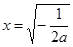 为函数
为函数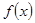 的唯一极大值点,
的唯一极大值点,
所以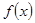 的最大值为
的最大值为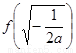 =
=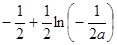 .
……8分
.
……8分
由题意有 ,解得
,解得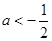 .
.
所以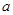 的取值范围为
的取值范围为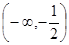 .
……10分
.
……10分
(Ⅲ)当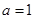 时,
时,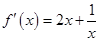 . 记
. 记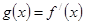 ,其中
,其中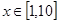 .
.
∵当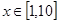 时,
时,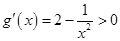 ,∴
,∴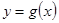 在
在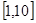 上为增函数,
上为增函数,
即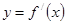 在
在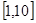 上为增函数.
……12分
上为增函数.
……12分
又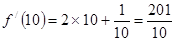 ,所以,对任意的
,所以,对任意的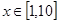 ,总有
,总有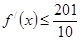 .
.
所以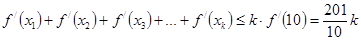 ,
,
又因为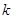
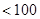 ,所以
,所以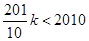 .
.
故在区间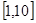 上不存在使得
上不存在使得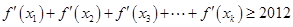 成立的
成立的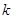 (
(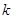
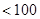 )个正数
)个正数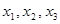 …
…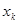 .
……14分
.
……14分
考点:本小题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想及有限与无限思想.
点评:对于题目条件较复杂,设问较多的题目审题时,应该细致严谨,将题目条件条目化,一一分析,细心推敲.对于设问较多的题目,一般前面的问题较简单,问题难度阶梯式上升,先由条件将前面的问题正确解答,然后将前面问题的结论作为后面问题解答的条件,注意问题之间的相互联系,使问题化难为易,层层解决.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
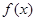 是定义在
是定义在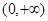 上的单调增函数,满足
上的单调增函数,满足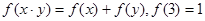 ,
,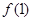 ;
;
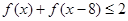 ,求
,求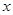 的取值范围。
的取值范围。