��Ŀ����
������{an}��{bn}�У���֪an=an��bn=(a+1)n+b��n=l��2��3����������a��2��a��N*��b��R��
(��)��a1=b1��a2��b2��������{bn}��ǰn��ͣ�
(��)֤������a=2��b=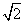 ʱ������{bn}�е�����������ܹ��ɵȱ����У�
ʱ������{bn}�е�����������ܹ��ɵȱ����У�
(��)�輯��A={a1��a2��a3����}��B={b1��b2��b3����}������������[1��a]���Ƿ����ʵ��bʹ��C=A��B�� �������ڣ����b��һ�п��ܵ�ȡֵ����Ӧ�ļ���C���������ڣ�˵�����ɡ�
�������ڣ����b��һ�п��ܵ�ȡֵ����Ӧ�ļ���C���������ڣ�˵�����ɡ�
(��)��a1=b1��a2��b2��������{bn}��ǰn��ͣ�
(��)֤������a=2��b=
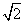 ʱ������{bn}�е�����������ܹ��ɵȱ����У�
ʱ������{bn}�е�����������ܹ��ɵȱ����У�(��)�輯��A={a1��a2��a3����}��B={b1��b2��b3����}������������[1��a]���Ƿ����ʵ��bʹ��C=A��B��
 �������ڣ����b��һ�п��ܵ�ȡֵ����Ӧ�ļ���C���������ڣ�˵�����ɡ�
�������ڣ����b��һ�п��ܵ�ȡֵ����Ӧ�ļ���C���������ڣ�˵�����ɡ� �⣺(��)��Ϊa1=b1������a=a+1+b��b=-1��
��a2��b2����a2-2a-1��0�� ����1-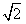 ��a��1+
��a��1+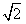 ��
��
��Ϊa��2��a��N*������a=2������bn=3n-1��{bn}�ǵȲ����У�
��������{bn}��ǰn���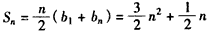 ��
��
(��)����֪bn=3n+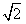 ��
��
����3m+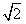 ��3n+
��3n+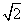 ��3t+
��3t+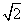 �ɵȱ����У�����m��n��t��N*���ұ˴˲��ȣ�
�ɵȱ����У�����m��n��t��N*���ұ˴˲��ȣ�
��3m+ ��2=��3m+
��2=��3m+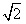 ����3t+
����3t+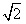 ����
����
����9n2+6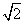 n+2=9mt+3
n+2=9mt+3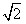 m+3
m+3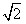 t+2��
t+2��
����3n2-3mt=(m+t-2n)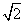 ��
��
��m+t-2n=0����3n2-3mt=0���ɵ�m=t����m��tì�ܣ�
��m+l-2n��0����m+t-2n����������(m+t-2n)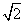 ��������
��������
����3n2-3mtΪ����������3n2-3mt������ì�ܣ�
��������{bn}�е�����������ܹ��ɵȱ����С�
(��)�����ʵ��b��[1��a]��ʹC=A��B�� ��
��
��m0��C����m0��A����m0��B��
��m0=at(t��N*)��m0=��a+1��s+b(s��N*)��
��at=��a+1��s+b������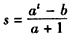 ��
��
��Ϊa��t��s��N*����a��2������at-b�ܱ�a+1������
(1)��t=1ʱ����Ϊb��[1��a]��a-b��[0��a-1]�����ԣ�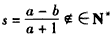 ��
��
(2)��t=2n(n��N*)ʱ��
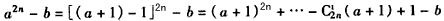 ��
��
����b��[1��a]��b-1��[0��a-1]��0��b-1��a+1��
���ԣ����ҽ���b=1ʱ��at-b�ܱ�a+1������
(3)��t=2n+1(n��N*)ʱ��
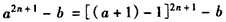
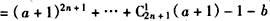 ��
��
����b��[1��a]��b+1��[2��a+1]��
���ԣ����ҽ���b+1=a+1����b=aʱ��at-b�ܱ�a+1������
���ϣ�������[1��a]�ϴ���ʵ��b��ʹC=A��B�� ������
������
�ҵ�b=1ʱ��C={y|y=a2n��n��N*}��
��b=aʱ��c={y|y=a2n+1��n��N*}��
��a2��b2����a2-2a-1��0�� ����1-
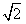 ��a��1+
��a��1+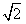 ��
�� ��Ϊa��2��a��N*������a=2������bn=3n-1��{bn}�ǵȲ����У�
��������{bn}��ǰn���
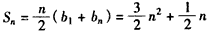 ��
��(��)����֪bn=3n+
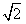 ��
������3m+
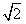 ��3n+
��3n+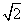 ��3t+
��3t+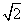 �ɵȱ����У�����m��n��t��N*���ұ˴˲��ȣ�
�ɵȱ����У�����m��n��t��N*���ұ˴˲��ȣ���3m+
 ��2=��3m+
��2=��3m+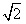 ����3t+
����3t+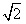 ����
��������9n2+6
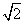 n+2=9mt+3
n+2=9mt+3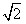 m+3
m+3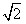 t+2��
t+2������3n2-3mt=(m+t-2n)
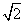 ��
����m+t-2n=0����3n2-3mt=0���ɵ�m=t����m��tì�ܣ�
��m+l-2n��0����m+t-2n����������(m+t-2n)
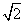 ��������
Ϊ������������3n2-3mtΪ����������3n2-3mt������ì�ܣ�
��������{bn}�е�����������ܹ��ɵȱ����С�
(��)�����ʵ��b��[1��a]��ʹC=A��B��
 ��
����m0��C����m0��A����m0��B��
��m0=at(t��N*)��m0=��a+1��s+b(s��N*)��
��at=��a+1��s+b������
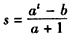 ��
����Ϊa��t��s��N*����a��2������at-b�ܱ�a+1������
(1)��t=1ʱ����Ϊb��[1��a]��a-b��[0��a-1]�����ԣ�
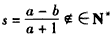 ��
��(2)��t=2n(n��N*)ʱ��
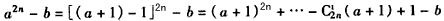 ��
������b��[1��a]��b-1��[0��a-1]��0��b-1��a+1��
���ԣ����ҽ���b=1ʱ��at-b�ܱ�a+1������
(3)��t=2n+1(n��N*)ʱ��
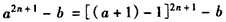
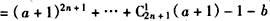 ��
������b��[1��a]��b+1��[2��a+1]��
���ԣ����ҽ���b+1=a+1����b=aʱ��at-b�ܱ�a+1������
���ϣ�������[1��a]�ϴ���ʵ��b��ʹC=A��B��
 ������
�������ҵ�b=1ʱ��C={y|y=a2n��n��N*}��
��b=aʱ��c={y|y=a2n+1��n��N*}��

��ϰ��ϵ�д�
�����Ŀ
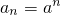 ��bn=��a+1��n+b��n=1��2��3����������a��2��a��N*��b��R��
��bn=��a+1��n+b��n=1��2��3����������a��2��a��N*��b��R��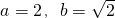 ʱ������{bn}�е�����������ܹ��ɵȱ����У�
ʱ������{bn}�е�����������ܹ��ɵȱ����У�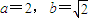 ʱ������{bn}�е�����������ܹ��ɵȱ����У�
ʱ������{bn}�е�����������ܹ��ɵȱ����У�