题目内容
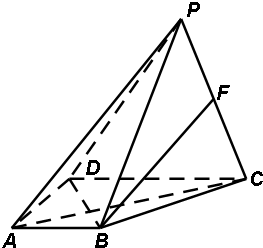 如图,四棱锥P-ABCD的底面是直角梯形,其中AB=
如图,四棱锥P-ABCD的底面是直角梯形,其中AB=
| ||
| 2 |
| 2 |
(Ⅰ)求证:BF∥平面PAD;
(Ⅱ)求证:平面PAC⊥平面PDB;
(Ⅲ)若PA=PC=1,求三棱锥P-DBF的体积.
分析:(I)取PD中点E,连结EA、EF,∵E、F分别是PD、PC的中点,可证四边形EFBA是平行四边形,AE∥BF,由线面平行的判定定理可证EF∥平面PAD;
(II)顶点P在底面ABCD的射影落在线段AC上,设为H,则PH⊥面ABCD,可得PH⊥BD,再证BD⊥面PAC,由面面垂直的判定定理证明平面PBD⊥平面PAC;
(III)由PA=PC=1,得H为AC的中点,根据VP-DBF=
VP-BCD,求出底面△BCD的面积和高AH,代入公式计算可得答案.
(II)顶点P在底面ABCD的射影落在线段AC上,设为H,则PH⊥面ABCD,可得PH⊥BD,再证BD⊥面PAC,由面面垂直的判定定理证明平面PBD⊥平面PAC;
(III)由PA=PC=1,得H为AC的中点,根据VP-DBF=
| 1 |
| 2 |
解答:解:(Ⅰ)证明:取PD中点E,连结EA、EF,
∵E、F分别是PD、PC的中点,
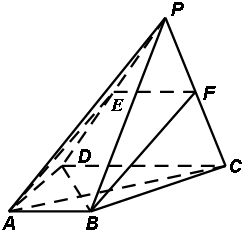
∴EF∥DC,又DC∥AB,且EF=
DC=AB,
∴EF∥AB,且EF=AB
∴四边形EFBA是平行四边形,∴AE∥BF,
又∵AE?面PAD,BF?面PAD,
∴EF∥平面PAD;
(II)证明:顶点P在底面ABCD的射影落在线段AC上,设为H,则PH⊥平面ABCD,
∵BD?平面ABCD,∴PH⊥BD,
∵Rt△ABD中,
=
,Rt△DAC中,
=
=
,
∴Rt△ABD∽Rt△DAC,
∴∠DAC=∠ABD,故∠ABD+∠CAB=90°即AC⊥BD,
又∵PH∩AC=H,PH、AC?平面PAC,∴BD⊥平面PAC,
BD?平面PBD,∴平面PBD⊥平面PAC;
( III)∵PA=PC=1,
∴顶点P在底面ABCD的射影H落在线段AC的中点上,且,AC=
=
,
∴S△BCD=S△ACD=
×1×
,AH=
=
,
∵F分别是PC的中点,∵F到面PDB的距离是C到面PDB的距离的
,
VP-DBF=
VC-PDB=
VP-DBC=
×
×(
×
×1)×
=
.
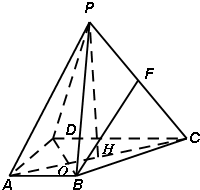
∵E、F分别是PD、PC的中点,

∴EF∥DC,又DC∥AB,且EF=
| 1 |
| 2 |
∴EF∥AB,且EF=AB
∴四边形EFBA是平行四边形,∴AE∥BF,
又∵AE?面PAD,BF?面PAD,
∴EF∥平面PAD;
(II)证明:顶点P在底面ABCD的射影落在线段AC上,设为H,则PH⊥平面ABCD,
∵BD?平面ABCD,∴PH⊥BD,
∵Rt△ABD中,
| AB |
| AD |
| ||
| 2 |
| AD |
| DC |
| 1 | ||
|
| ||
| 2 |
∴Rt△ABD∽Rt△DAC,
∴∠DAC=∠ABD,故∠ABD+∠CAB=90°即AC⊥BD,
又∵PH∩AC=H,PH、AC?平面PAC,∴BD⊥平面PAC,
BD?平面PBD,∴平面PBD⊥平面PAC;
( III)∵PA=PC=1,
∴顶点P在底面ABCD的射影H落在线段AC的中点上,且,AC=
| 1+2 |
| 3 |
∴S△BCD=S△ACD=
| 1 |
| 2 |
| 2 |
1-(
|
| 1 |
| 2 |
∵F分别是PC的中点,∵F到面PDB的距离是C到面PDB的距离的
| 1 |
| 2 |
VP-DBF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 24 |

点评:本题考查了线面平行的判定,考查了面面垂直的判定,考查了学生的空间想象能力与推理运算能力,体现了转化思想.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=