题目内容
如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
(3)在所给直观图中连接BC′,证明:BC′∥面EFG.
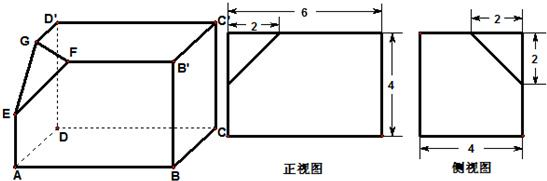
分析:(1)按照三视图的要求直接在正视图下面,画出该多面体的俯视图;
(2)按照给出的尺寸,利用转化思想V=V长方体-V正三棱锥,求该多面体的体积;
(3)在长方体ABCD-A′B′C′D′中,连接AD′,在所给直观图中连接BC′,证明EG∥BC′,即可证明BC′∥面EFG.
(2)按照给出的尺寸,利用转化思想V=V长方体-V正三棱锥,求该多面体的体积;
(3)在长方体ABCD-A′B′C′D′中,连接AD′,在所给直观图中连接BC′,证明EG∥BC′,即可证明BC′∥面EFG.
解答:解:(1)如图
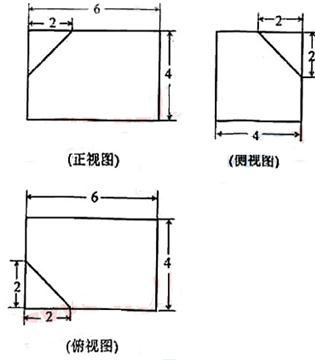
(2)所求多面体的体积V=V长方体-V正三棱锥=4×4×6-
×(
×2×2)×2=
(cm3)
(3)证明:如图,
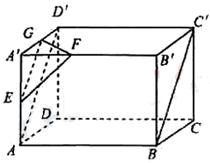
在长方体ABCD-A′B′C′D′中,连接AD′,则AD′∥BC′
因为E,G分别为AA′,A′D′中点,所以AD′∥EG,从而EG∥BC′,
又EG?平面EFG,所以BC′∥平面EFG;

(2)所求多面体的体积V=V长方体-V正三棱锥=4×4×6-
| 1 |
| 3 |
| 1 |
| 2 |
| 284 |
| 3 |
(3)证明:如图,

在长方体ABCD-A′B′C′D′中,连接AD′,则AD′∥BC′
因为E,G分别为AA′,A′D′中点,所以AD′∥EG,从而EG∥BC′,
又EG?平面EFG,所以BC′∥平面EFG;
点评:长方体的有关知识、体积计算及三视图的相关知识,对三视图的相关知识掌握不到位,求不出有关数据.三视图是新教材中的新内容,故应该是新高考的热点之一,要予以足够的重视.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目





 )
) ,证明:
,证明:
