题目内容
(本题满分12分)设函数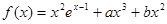 ,已知
,已知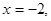 和
和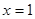 为
为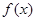 的极值点。
的极值点。
(I)求a和b的值;
(II)设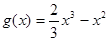 ,试证
,试证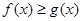 恒成立。
恒成立。
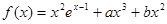 ,已知
,已知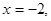 和
和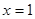 为
为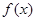 的极值点。
的极值点。(I)求a和b的值;
(II)设
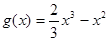 ,试证
,试证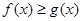 恒成立。
恒成立。解:(I)
又 和
和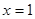 为
为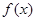 的极值点
的极值点
即 解之,得
解之,得 (4分)
(4分)

当 时,
时, ,此时
,此时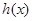 在区间
在区间 内是增函数
内是增函数 (10分)
(10分)
综上,对任意实数x都有 ,又
,又
所以,对任意实数x都有 ,即
,即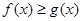 恒成立。(12分)
恒成立。(12分)

又
 和
和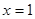 为
为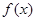 的极值点
的极值点
即
 解之,得
解之,得 (4分)
(4分)
当
 时,
时, ,此时
,此时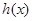 在区间
在区间 内是增函数
内是增函数 (10分)
(10分)综上,对任意实数x都有
 ,又
,又
所以,对任意实数x都有
 ,即
,即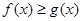 恒成立。(12分)
恒成立。(12分)略

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
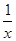 )′=1+
)′=1+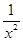

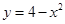 与直线
与直线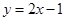 的两个交点为
的两个交点为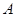 、
、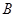 ,点
,点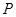 在抛物弧上从
在抛物弧上从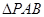 的面积最大的点
的面积最大的点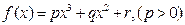 图象的对称中心为
图象的对称中心为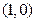 ,且
,且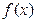 的极小值为
的极小值为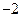 .
.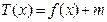 ,若
,若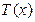 有三个零点,求实数
有三个零点,求实数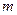 的取值范围;
的取值范围;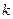 ,当
,当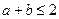 时,使函数
时,使函数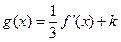
 上的函数
上的函数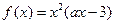 ,其中
,其中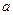 为常数.
为常数.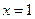 是函数
是函数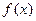 的一个极值点,求
的一个极值点,求 间
间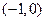 上是增函数,求
上是增函数,求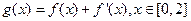 ,在
,在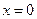 处取得最大值,求正数
处取得最大值,求正数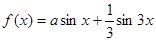 ,在
,在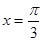 处有极值,则
处有极值,则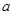 等于( )
等于( )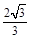
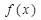 的导函数为
的导函数为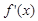 ,且
,且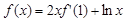 ,则
,则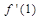 = .
= . ,那么
,那么 .
.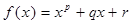 ,
,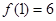 ,
,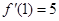 ,
,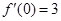 ,
,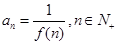 ,则数列
,则数列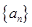 的前
的前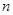 项和是
项和是