题目内容
已知A、B是双曲线x2-(1)当α=![]() ,且
,且![]() =(2,
=(2,![]() )时,求P点的坐标;
)时,求P点的坐标;
(2)当![]() ·
·![]() =0时,求|
=0时,求|![]() |的值;
|的值;
(3)求|AB|的最小值.
解:(1)设![]() =(x,y),则由
=(x,y),则由![]() ·
·![]() =0及点B在双曲线上,得
=0及点B在双曲线上,得

解得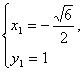 或
或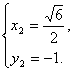
∴![]() =(-
=(-![]() ,1)或
,1)或![]() =(
=(![]() ,-1).
,-1).
∴![]() =
=![]()
![]() +
+![]()
![]() =(
=(![]() ,
,![]() )或
)或
![]() =
=![]()
![]() +
+![]()
![]() =(
=(![]() ,
,![]() ),
),
即P点的坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
(2)设直线OA的方程为y=kx,则由
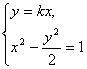 得x2=
得x2=![]() ,y2=
,y2=![]() .
.
∴|OA|2=x2+y2=![]() .
.
同理,可得|OB|2=![]() .
.
由|OP|·|AB|=|OA|·|OB|,得![]() =
=![]() =
=![]() +
+![]() =
=![]() .
.
∴|OP|=![]() .
.
(3)方法一:由|OP|·|AB|=|OA|·|OB|,![]() =
=![]() =
=![]() ,
,
(|OA|2+|OB|2)(![]() )≥4,
)≥4,
∴|AB|2≥8.故|AB|≥2![]() ,当且仅当|OA|=|OB|=2时,等号成立.
,当且仅当|OA|=|OB|=2时,等号成立.
故|AB|的最小值为2![]() .
.
方法二:由(2)知|AB|2=3〔|AB|2=3(x12+x22)-4,3x12x22=4(x12+x22)-4〕.
设a=x12,b=x22,则a>0,b>0,ab≤(![]() )2,
)2,
4(a+b)-4≤3(![]() )2,a+b≥4或a+b≤
)2,a+b≥4或a+b≤![]() .
.
当a+b≤![]() 时,|AB|2≤0(不合,舍去);
时,|AB|2≤0(不合,舍去);
当a+b≥4时,|AB|2=3(a+b)-4≥8,|AB|≥2![]() ,当且仅当a=b=2,即x1=x2=±
,当且仅当a=b=2,即x1=x2=±![]() 时取等号.
时取等号.
故|AB|的最小值为2![]() .
.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目