题目内容
平面内n条直线,其中任何两条不平行,任何三条不共点.
(1)设这n条直线互相分割成f(n)条线段或射线,猜想f(n)的表达式并给出证明;
(2)求证:这n条直线把平面分成
+1个区域.
(1)设这n条直线互相分割成f(n)条线段或射线,猜想f(n)的表达式并给出证明;
(2)求证:这n条直线把平面分成
| n(n+1) |
| 2 |
(1)f(2)=4,f(3)=9,f(4)=16,.
∴猜想f(n)=n2.以下用数学归纳法证明:①当n=2时,f(2)=4=22,猜想正确.
②假设n=k(k≥2)时猜想正确,即f(k)=k2,
则当n=k+1时,这第k+1条直线与原来的k条直线分别相交,新增k个交点,
它们分别把原来的一条线段或射线一分为二,
使原来的k条直线新分割出k条线段或射线,
又这k个交点还把第k+1条直线分割为k+1条线段或射线.
∴当n=k+1时,猜想也正确.
根据①②知,对大于1的任意自然数n,猜想都正确.
(2)证明:①当n=1时,一条直线把平面分为两部分,
而n=1时
+1=2,∴n=1时命题正确.
②假设n=k时命题正确,即k条直线把平面分成
+1个区域,
则n=k+1时,第k+1条直线被原来的k条直线截成k+1条线段或射线,
而每一条线段或射线都把它们所占的一块区域一分为二,
故新增加出k+1块区域,
因此k+1条直线把平面共分成
+(k+1)+1,即
+1个区域.
∴当n=k+1时命题也成立.
由①②可知,对任意的n∈N*,命题都成立.
∴猜想f(n)=n2.以下用数学归纳法证明:①当n=2时,f(2)=4=22,猜想正确.
②假设n=k(k≥2)时猜想正确,即f(k)=k2,
则当n=k+1时,这第k+1条直线与原来的k条直线分别相交,新增k个交点,
它们分别把原来的一条线段或射线一分为二,
使原来的k条直线新分割出k条线段或射线,
又这k个交点还把第k+1条直线分割为k+1条线段或射线.
∴当n=k+1时,猜想也正确.
根据①②知,对大于1的任意自然数n,猜想都正确.
(2)证明:①当n=1时,一条直线把平面分为两部分,
而n=1时
| n(n+1) |
| 2 |
②假设n=k时命题正确,即k条直线把平面分成
| k(k+1) |
| 2 |
则n=k+1时,第k+1条直线被原来的k条直线截成k+1条线段或射线,
而每一条线段或射线都把它们所占的一块区域一分为二,
故新增加出k+1块区域,
因此k+1条直线把平面共分成
| k(k+1) |
| 2 |
| (k+1)(k+2) |
| 2 |
∴当n=k+1时命题也成立.
由①②可知,对任意的n∈N*,命题都成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
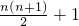 个区域.
个区域.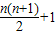 个区域.
个区域.