题目内容
(2011•顺义区二模)设函数f(x)=ax3-
x2+c,其图象过点(0,1).
(1)当方程f′(x)-x+1=0的两个根分别为是
,1时,求f(x)的解析式;
(2)当a=
,b≠0时,求函数f(x)的极大值与极小值.
| b |
| 2 |
(1)当方程f′(x)-x+1=0的两个根分别为是
| 1 |
| 2 |
(2)当a=
| 2 |
| 3 |
分析:(1)先求函数f(x)的导函数f′(x),依题意f(0)=1,方程f′(x)-x+1=0的两个根分别为是
,1,列方程求解即可得a、b、c的值
(2)先求函数f(x)的导函数f′(x)=2x(x-
),研究函数的单调性需要讨论b的正负,故分b>0和b<0两种情况分别讨论函数的单调性和极值即可
| 1 |
| 2 |
(2)先求函数f(x)的导函数f′(x)=2x(x-
| b |
| 2 |
解答:解:由题意可知,f(0)=1所以c=1
(1)由f(x)=ax3-
x2+1,得f′(x)=3ax2-bx.
因为f′(x)-x+1=0,即3ax2-bx-x+1=0的两个根分别为
,1
所以
解得
故f(x)=
x3-x2+1
(Ⅱ)f(x)=
x3-
x2+c
所以,f′(x)=2x2-bx=2x(x-
)
①若b>0,则当x∈(-∞,0)时,f′(x)>0函数f(x)单调递增;
当x∈(0,
)时,f′(x)<0函数f(x)单调递减;
当x∈(
,+∞)时,f′(x)>0函数f(x)单调递增
因此,f(x)的极大值为f(0)=c=1,f(x)的极小值为f(
)=1-
②若b<0,则当x∈(-∞,
)时,f′(x)>0函数f(x)单调递增;
当x∈(
,0)时,f′(x)<0函数f(x)单调递减;
当x∈(0,+∞)时,f′(x)>0函数f(x)单调递增
因此,f(x)的极大值为f(
)=1-
,f(x)的极小值为f(0)=1.
综上所述,当b>0时,f(x)的极大值为1,极小值为1-
,
当b<0时,f(x)的极大值为1-
,极小值为
(1)由f(x)=ax3-
| b |
| 2 |
因为f′(x)-x+1=0,即3ax2-bx-x+1=0的两个根分别为
| 1 |
| 2 |
所以
|
解得
|
故f(x)=
| 2 |
| 3 |
(Ⅱ)f(x)=
| 2 |
| 3 |
| b |
| 2 |
所以,f′(x)=2x2-bx=2x(x-
| b |
| 2 |
①若b>0,则当x∈(-∞,0)时,f′(x)>0函数f(x)单调递增;
当x∈(0,
| b |
| 2 |
当x∈(
| b |
| 2 |
因此,f(x)的极大值为f(0)=c=1,f(x)的极小值为f(
| b |
| 2 |
| b3 |
| 24 |
②若b<0,则当x∈(-∞,
| b |
| 2 |
当x∈(
| b |
| 2 |
当x∈(0,+∞)时,f′(x)>0函数f(x)单调递增
因此,f(x)的极大值为f(
| b |
| 2 |
| b3 |
| 24 |
综上所述,当b>0时,f(x)的极大值为1,极小值为1-
| b3 |
| 24 |
当b<0时,f(x)的极大值为1-
| b3 |
| 24 |
点评:本题考察了导数在函数单调性和极值中的应用,分类讨论的思想方法

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
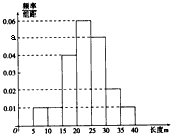 (2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=
(2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=