题目内容
某校共有学生2000名，各年级男、女生人数如表所示．已知在全校学生中随机抽取1名，抽到二年级女生的概率是0.19．现用分层抽样的方法在全校抽取64名学生，则应在三年级抽取的学生人数为( )
| A．24 | B．18 | C．16 | D．12 |
C
解析
练习册系列答案
阅读快车系列答案
相关题目
为调查参加运动会的1000名运动员的年龄情况，从中抽查了100名运动员的年龄作为样
本，就这个问题来说，下列说法正确的是( )
| A．1000名运动员是总体 | B．每个运动员是个体 |
| C．抽取的100名运动员的年龄是样本 | D．样本容量是1000 |
对总数为N的一批零件抽取一个容量为30的样本，若每个零件被抽到的概率为0.25， 则N的值为
| A．120 | B．200 | C．150 | D．100 |
经统计,某地的财政收入
与支出
满足的线性回归模型是
(单位:亿元),其中
为随机误差,如果今年该地区财政收入10亿元,则年支出预计不超出( )
| A．10亿 | B．11亿 | C．11.5亿 | D．12亿 |
某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下：
| | | | | | 甲 | | 乙 | | | | | |
| | | | 9 | 8 | 8 | 1 | 7 | 7 | 9 | 9 | | |
| | | | 6 | 1 | 0 | 2 | 2 | 5 | 6 | 7 | 9 | 9 |
| | | 5 | 3 | 2 | 0 | 3 | 0 | 2 | 3 | | | |
| | | | 7 | 1 | 0 | 4 | | | | | | |
A．甲运动员得分的极差大于乙运动员得分的极差
B．甲运动员得分的的中位数大于乙运动员得分的的中位数
C．甲运动员的得分平均值大于乙运动员的得分平均值
D．甲运动员的成绩比乙运动员的成绩稳定
对甲、乙的学习成绩进行抽样分析，各抽五门功课，得到的观测值如下：
| 甲 | 60 | 80 | 70 | 90 | 70 |
| 乙 | 80 | 60 | 70 | 80 | 75 |
A. 甲的平均成绩较好，乙的各门功课发展较平衡
B. 甲的平均成绩较好，甲的各门功课发展较平衡
C. 乙的平均成绩较好，甲的各门功课发展较平衡
D. 乙的平均成绩较好，乙的各门功课发展较平衡
对变量x, y 有观测数据理力争（
，
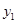）（i=1,2,…，10），得散点图1；对变量u ，v 有观测数据（
，
）（i=1,2,…，10）,得散点图2. 由这两个散点图可以判断。
| A．变量x 与y 正相关，u 与v 正相关 | B．变量x 与y 正相关，u 与v 负相关 |
| C．变量x 与y 负相关，u 与v 正相关 | D．变量x 与y 负相关，u 与v 负相关 |
已知回归直线的斜率的估计值是1.23，样本点的中心为(4,5)，则回归直线的方程是( )
A． | B． |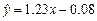
C． | D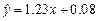． |