题目内容
(本小题满分14分)
如图,在四棱锥 中,底面
中,底面 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形, 与
与 的交点为
的交点为 ,
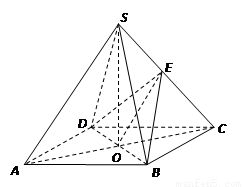
, 为侧棱
为侧棱 上一点.
上一点.

(Ⅰ)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(Ⅱ)求证:平面BDE⊥平面SAC
【答案】
证明:(Ⅰ)见解析;(Ⅱ)见解析。
【解析】本试题主要是考查了立体几何中线面平行的证明以及面面垂直的证明的综合运用。
(1)利用线面平行的判定定理可知知道,解决SA∥OE的平行时关键的一步。
(2)要证明面面垂直,只要证明线面垂直的基础上,利用面面垂直的判定定理既可以得到。
证明:(Ⅰ)连接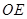 ,---------------1分
,---------------1分
∵点O、E分别为AC、SC中点
∴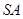 ∥
∥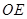 ---------------3分
---------------3分
∵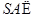 平面
平面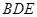 ,
,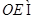 平面
平面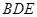 ,---------------5分
,---------------5分
∴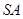 ∥平面
∥平面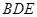 .--------------7分
.--------------7分
(Ⅱ)由已知可得,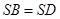 ,
,
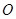 是
是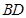 中点,所以
中点,所以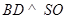 .-------------9分
.-------------9分
又∵四边形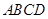 是正方形,
是正方形,
∴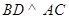 .----------------10分
.----------------10分
∵ ,∴
,∴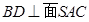 .--------------12分
.--------------12分
∵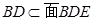 ,
,
∴平面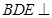 平面
平面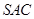 .------------14分
.------------14分

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)