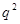题目内容
设ξ是一个离散型随机变量,其分布列如下表,试求Eξ、Dξ.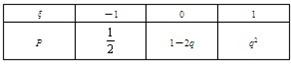
分析:应先按分布列的性质在这个分布列中所有的概率之和是1,列出关于q的一元二次方程,解方程求出q的值后,那么本题的分布列就写出来了,再根据期望和方差的公式计算出Eξ、Dξ.
解答:解:∵随机变量的概率非负且随机变量取遍所有可能值时相应的概率之和等于1,
∴
解得q=1-
.
∴ξ的分布列为
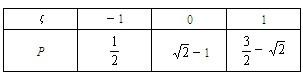
∴Eξ=(-1)×
+0×(
-1)+1×(
-
)=1-
,
Dξ=[-1-(1-
)]2×
+(1-
)2×(
-1)+[1-(1-
)]2×(
-
)=
-1.
∴
|
| ||
| 2 |
∴ξ的分布列为

∴Eξ=(-1)×
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
Dξ=[-1-(1-
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
点评:解答本题时应防止机械地套用期望和方差的计算公式,出现以下误解:Eξ=(-1)×
+0×(1-2q)+1×q2=q2-
.要根据概率的性质作出q的值,再求出结果.
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
设X是一个离散型随机变量,其分布列如图,则q等于( )
| x | -1 | 0 | 1 |
| P | 0.5 | 1-2q | q2 |
| A、1 | ||||
B、1±
| ||||
C、1-
| ||||
D、1+
|