题目内容
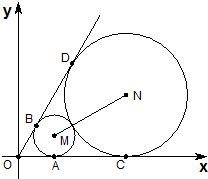 如图,已知圆心坐标为M(
如图,已知圆心坐标为M(| 3 |
| 3 |
| 3 |
(1)求⊙M和⊙N的方程;
(2)过点B作直线MN的平行线l,求直线l被⊙N截得的弦的长度.
分析:(1)连接MA,根据⊙M与x轴相切得MA⊥OA,根据圆心坐标M(
,1)得到圆的半径为1,写出⊙M的方程;设出⊙N的半径r,利用相似求出r,并求出圆心N的坐标,即可得到⊙N的方程;
(2)由对称性可知,所求的弦长等于过点A且与直线MN平行的直线被⊙N截得的弦长,根据点A的坐标和直线MN的斜率求出弦长的方程,然后利用点到直线的距离公式求出圆心N到弦的弦心距,然后利用勾股定理即可求出弦.
| 3 |
(2)由对称性可知,所求的弦长等于过点A且与直线MN平行的直线被⊙N截得的弦长,根据点A的坐标和直线MN的斜率求出弦长的方程,然后利用点到直线的距离公式求出圆心N到弦的弦心距,然后利用勾股定理即可求出弦.
解答:解:(1)由于⊙M与∠BOA的两边均相切,故M到OA及OB的距离均为⊙M的半径,则M在∠BOA的平分线上,
同理,N也在∠BOA的平分线上,即O,M,N三点共线,且OMN为∠BOA的平分线;
∵M的坐标为(
,1),
∴M到x轴的距离为1,即⊙M的半径为1,
∴⊙M的方程为(x-
)2+(y-1)2=1,
设⊙N的半径为r,其与x轴的切点为C,连接MA、MC,
由Rt△OAM∽Rt△OCN可知,OM:ON=MA:NC,
即
=
,解得r=3;
∴OC=3
,点N坐标为(3
,3);
∴⊙N的方程为(x-3
)2+(y-3)2=9.
(2)由对称性可知,所求的弦长等于过点A且与直线MN平行的直线被⊙N截得的弦长,此弦的方程是y=
(x-
),即:x-
y-
=0,
∵圆心N到该弦的距离d=
,
∴所求弦长=2
=
.
同理,N也在∠BOA的平分线上,即O,M,N三点共线,且OMN为∠BOA的平分线;
∵M的坐标为(
| 3 |
∴M到x轴的距离为1,即⊙M的半径为1,
∴⊙M的方程为(x-
| 3 |
设⊙N的半径为r,其与x轴的切点为C,连接MA、MC,
由Rt△OAM∽Rt△OCN可知,OM:ON=MA:NC,
即
| 2 |
| 3+r |
| 1 |
| r |
∴OC=3
| 3 |
| 3 |
∴⊙N的方程为(x-3
| 3 |
(2)由对称性可知,所求的弦长等于过点A且与直线MN平行的直线被⊙N截得的弦长,此弦的方程是y=
| ||
| 3 |
| 3 |
| 3 |
| 3 |
∵圆心N到该弦的距离d=
| ||
| 2 |
∴所求弦长=2
| r2-d2 |
| 33 |
点评:这是一道直线与圆的方程的综合运用题,主要考查学生会利用垂径定理得直角三角形求弦长的方法,同时要求学生掌握点到直线的距离公式.

练习册系列答案
相关题目
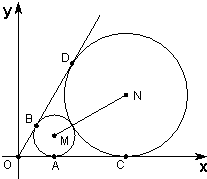 如图,已知圆心坐标为(
如图,已知圆心坐标为( 的圆
的圆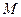 与
与 轴及直线
轴及直线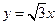 分别相切于
分别相切于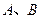 两点,另一圆
两点,另一圆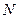 与圆
与圆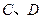 两点.
两点.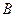 作直线
作直线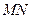 的平行线
的平行线 ,求直线
,求直线
 的圆
的圆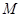 与
与 轴及直线
轴及直线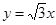 均相切,切点分别为
均相切,切点分别为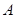 、
、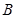 ,另一圆
,另一圆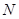 与圆
与圆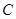 、
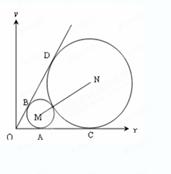
、 .
.
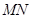 的平行线
的平行线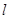 ,求直线
,求直线 的圆
的圆 与
与 轴及直线
轴及直线 分别相切于
分别相切于 两点,另一圆
两点,另一圆 与圆
与圆 两点.
两点. 作直线
作直线 的平行线
的平行线 ,求直线
,求直线