题目内容
若不等式x2+ax+1≥0对一切
成立，则a的最小值为（ ）
成立，则a的最小值为（ ）| A．0 | B．﹣2 | C． | D．﹣3 |
C
设f（x）=x2+ax+1，则对称轴为x=
若≥
，即a≤﹣1时，则f（x）在〔0，〕上是减函数，
应有f（）≥0⇒﹣
≤a≤﹣1
若≤0，即a≥0时，则f（x）在〔0，〕上是增函数，
应有f（0）=1＞0恒成立，
故a≥0
若0≤≤
，即﹣1≤a≤0，
则应有f（
）=
恒成立，
故﹣1≤a≤0
综上，有﹣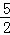
≤a．
故选C
若
≥，即a≤﹣1时，则f（x）在〔0，〕上是减函数，应有f（
）≥0⇒﹣≤a≤﹣1若
≤0，即a≥0时，则f（x）在〔0，〕上是增函数，应有f（0）=1＞0恒成立，
故a≥0
若0≤
≤，即﹣1≤a≤0，则应有f（
）=恒成立，故﹣1≤a≤0
综上，有﹣
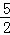≤a．故选C
练习册系列答案
阅读快车系列答案
相关题目
；
的不等式: 
.
R，a2＋2b2＋3c2＝6，求a＋b＋c的最大值．
；
＋
)≥4；
≥a＋b；
≥－2.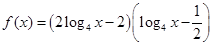
。
时，求该函数的值域；
对于
恒成立，求
的取值范围.
，b=
，c=log32则a，b，c的大小关系是（ ）
，则函数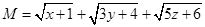
的最大值为 ．