题目内容
已知圆M:(x+| 5 |
| 5 |
| NP |
| NQ |
| GQ |
| NP |
(I)求点G的轨迹C的方程;
(II)过点(2,0)作直线l,与曲线C交于A、B两点,O是坐标原点,设
| OS |
| OA |
| OB |
分析:(I)点Q在NP上,点G在MP上,且满足
=2
,
•
=0故有|GN|+|GM|=|MP|=6,由椭圆的定义知G点的轨迹是以M、N为焦点的椭圆,由定义写出其标准方程即可得到点G的轨迹C的方程.
(II)
=
+
,所以四边形OASB为平行四边形,若存在l使得|
|=|
|,则四边形OASB必为矩形即有
•
=0,令A(x1,y1),B(x2,y2),则有x1x2+y1y2=0,由直线l与曲线C联立求利用根与系数的关系求出x1x2,y1y2的参数表达式,代入求直线的斜率k,若能求出,则说明存在,若不能求出,则不存在.
| NP |
| NQ |
| GQ |
| NP |
(II)
| OS |
| OA |
| OB |
| OS |
| AB |
| OA |
| OB |
解答:解:(I)
?Q为PN的中点且GQ⊥PN?GQ为PN的中垂线?|PG|=|GN|
∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长a=3,半焦距c=
,
∴短半轴长b=2,∴点G的轨迹方程是
+
=1(5分)
(II)因为
=
+
,所以四边形OASB为平行四边形
若存在l使得|
|=|
|,则四边形OASB为矩形∴
•
=0
若l的斜率不存在,直线l的方程为x=2,
由
得
∴
•
=
>0,与
•
=0矛盾,
故l的斜率存在.(7分)
设l的方程为y=k(x-2),A(x1,y1),B(x2,y2)
由
?(9k2+4)x2-36k2x+36(k2-1)=0
∴x1+x2=
,x1x2=
①
y1y2=[k(x1-2)][k(x2-2)]=k2[x1x2-2(x1+x2)+4]=-
②(9分)
把①、②代入x1x2+y1y2=0得k=±
∴存在直线l:3x-2y-6=0或3x+2y-6=0使得四边形OASB的对角线相等.
|
∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长a=3,半焦距c=
| 5 |
∴短半轴长b=2,∴点G的轨迹方程是
| x2 |
| 9 |
| y2 |
| 4 |
(II)因为
| OS |
| OA |
| OB |
若存在l使得|
| OS |
| AB |
| OA |
| OB |
若l的斜率不存在,直线l的方程为x=2,
由
|
|
| OA |
| OB |
| 16 |
| 9 |
| OA |
| OB |
故l的斜率存在.(7分)
设l的方程为y=k(x-2),A(x1,y1),B(x2,y2)
由
|
∴x1+x2=
| 36k2 |
| 9k2+4 |
| 36(k2-1) |
| 9k2+4 |
y1y2=[k(x1-2)][k(x2-2)]=k2[x1x2-2(x1+x2)+4]=-
| 20k2 |
| 9k2+4 |
把①、②代入x1x2+y1y2=0得k=±
| 3 |
| 2 |
∴存在直线l:3x-2y-6=0或3x+2y-6=0使得四边形OASB的对角线相等.
点评:本题的考点是轨迹方程,考查了定义法求椭圆的轨迹方程与直线与椭圆的相交问题,直线与椭圆的关系问题是圆锥曲线中一类常考的综合题,其规律是联立方程?消元得关于x,或y的一元二次方程,再利用根系关系得到两个直线的交点的坐标满足的方程,学习时应注意总结这一共性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
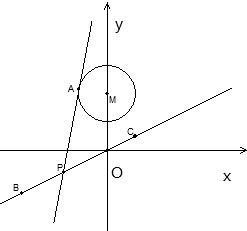 已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A
已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A