题目内容
已知函数f(x)=2sinxcosx+cos2x(x∈R).(1)当x取什么值时,函数f(x)取得最大值,并求其最大值;
(2)若θ为锐角,且
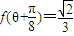 ,求tanθ的值.
,求tanθ的值.
【答案】分析:(1)由倍角公式,把2sinxcosx化为sin2x,再用换角化式把2x角化为2x+ 角,把这个角看成一个整体角X,利用正弦函数的有界性得最大值.
角,把这个角看成一个整体角X,利用正弦函数的有界性得最大值.
(2)把θ+ 代入f(x)的解析式得f(θ+
代入f(x)的解析式得f(θ+ )的解析式,
)的解析式,
①解法1,由f(θ+ )的解析式得cos2θ的值,由平方关系及θ角的范围得sin2θ的值,由商的关系得tan2θ,再由正切的二倍角公式得tanθ的二次方程,分解因式得tanθ的值,再由角的范围确定唯一的值.
)的解析式得cos2θ的值,由平方关系及θ角的范围得sin2θ的值,由商的关系得tan2θ,再由正切的二倍角公式得tanθ的二次方程,分解因式得tanθ的值,再由角的范围确定唯一的值.
②解法2,由f(θ+ )的解析式得cos2θ的值,由二倍角公式和θ角的范围得cosθ的值,由平方关系得sinθ的值,由商的关系得tanθ的值.
)的解析式得cos2θ的值,由二倍角公式和θ角的范围得cosθ的值,由平方关系得sinθ的值,由商的关系得tanθ的值.
③解法3,由f(θ+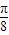 )的解析式得cos2θ的值,由平方关系及θ角的范围得sin2θ的值,由商的关系得tanθ,分子分母同乘以2cosθ,把角θ化为2θ,代数求值.
)的解析式得cos2θ的值,由平方关系及θ角的范围得sin2θ的值,由商的关系得tanθ,分子分母同乘以2cosθ,把角θ化为2θ,代数求值.
解答:解:(1)f(x)=2sinxcosx+cos2x=sin2x+cos2x(1分)
= (2分)
(2分)
=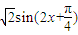 .(3分)
.(3分)
∴当 ,即
,即 Z)时,函数f(x)取得最大值,其值为
Z)时,函数f(x)取得最大值,其值为 .
.
(5分)
(2)解法1:∵ ,∴
,∴ .(6分)
.(6分)
∴ .(7分)
.(7分)
∵θ为锐角,即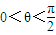 ,∴0<2θ<π.
,∴0<2θ<π.
∴ .(8分)
.(8分)
∴ .(9分)
.(9分)
∴ .(10分)
.(10分)
∴ .
.
∴ .
.
∴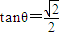 或
或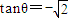 (不合题意,舍去)(11分)
(不合题意,舍去)(11分)
∴ .(12分)
.(12分)
解法2:∵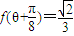 ,∴
,∴ .
.
∴ .(7分)
.(7分)
∴ .(8分)
.(8分)
∵θ为锐角,即 ,
,
∴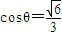 .(9分)
.(9分)
∴ .(10分)
.(10分)
∴ .(12分)
.(12分)
解法3:∵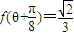 ,∴
,∴ .
.
∴ .(7分)
.(7分)
∵θ为锐角,即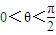 ,∴0<2θ<π.
,∴0<2θ<π.
∴ .(8分)
.(8分)
∴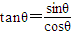 (9分)
(9分)
= (10分)
(10分)
=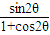 =
=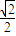 .(12分)
.(12分)
点评:本小题主要考查三角函数性质,同角三角函数的基本关系、两倍角公式等知识,执果索因,在未知和已知之间架好桥梁,考查化归与转化的数学思想方法和运算求解能力.
 角,把这个角看成一个整体角X,利用正弦函数的有界性得最大值.
角,把这个角看成一个整体角X,利用正弦函数的有界性得最大值.(2)把θ+
 代入f(x)的解析式得f(θ+
代入f(x)的解析式得f(θ+ )的解析式,
)的解析式,①解法1,由f(θ+
 )的解析式得cos2θ的值,由平方关系及θ角的范围得sin2θ的值,由商的关系得tan2θ,再由正切的二倍角公式得tanθ的二次方程,分解因式得tanθ的值,再由角的范围确定唯一的值.
)的解析式得cos2θ的值,由平方关系及θ角的范围得sin2θ的值,由商的关系得tan2θ,再由正切的二倍角公式得tanθ的二次方程,分解因式得tanθ的值,再由角的范围确定唯一的值.②解法2,由f(θ+
 )的解析式得cos2θ的值,由二倍角公式和θ角的范围得cosθ的值,由平方关系得sinθ的值,由商的关系得tanθ的值.
)的解析式得cos2θ的值,由二倍角公式和θ角的范围得cosθ的值,由平方关系得sinθ的值,由商的关系得tanθ的值.③解法3,由f(θ+
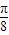 )的解析式得cos2θ的值,由平方关系及θ角的范围得sin2θ的值,由商的关系得tanθ,分子分母同乘以2cosθ,把角θ化为2θ,代数求值.
)的解析式得cos2θ的值,由平方关系及θ角的范围得sin2θ的值,由商的关系得tanθ,分子分母同乘以2cosθ,把角θ化为2θ,代数求值.解答:解:(1)f(x)=2sinxcosx+cos2x=sin2x+cos2x(1分)
=
 (2分)
(2分)=
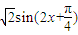 .(3分)
.(3分)∴当
 ,即
,即 Z)时,函数f(x)取得最大值,其值为
Z)时,函数f(x)取得最大值,其值为 .
.(5分)
(2)解法1:∵
 ,∴
,∴ .(6分)
.(6分)∴
 .(7分)
.(7分)∵θ为锐角,即
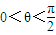 ,∴0<2θ<π.
,∴0<2θ<π.∴
 .(8分)
.(8分)∴
 .(9分)
.(9分)∴
 .(10分)
.(10分)∴
 .
.∴
 .
.∴
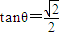 或
或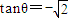 (不合题意,舍去)(11分)
(不合题意,舍去)(11分)∴
 .(12分)
.(12分)解法2:∵
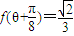 ,∴
,∴ .
.∴
 .(7分)
.(7分)∴
 .(8分)
.(8分)∵θ为锐角,即
 ,
,∴
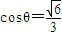 .(9分)
.(9分)∴
 .(10分)
.(10分)∴
 .(12分)
.(12分)解法3:∵
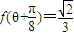 ,∴
,∴ .
.∴
 .(7分)
.(7分)∵θ为锐角,即
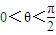 ,∴0<2θ<π.
,∴0<2θ<π.∴
 .(8分)
.(8分)∴
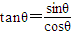 (9分)
(9分)=
 (10分)
(10分)=
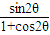 =
=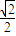 .(12分)
.(12分)点评:本小题主要考查三角函数性质,同角三角函数的基本关系、两倍角公式等知识,执果索因,在未知和已知之间架好桥梁,考查化归与转化的数学思想方法和运算求解能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目