题目内容
已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则直线PD与平面ABC所成的角为
.
| π |
| 4 |
| π |
| 4 |
分析:如图所示,不妨设AB=2,则PA=4,利用正六边形的性质即可得出AD的长,再利用线面垂直的性质和线面角的定义可知:∠PDA是直线PD与平面ABC所成的角.
解答:解:如图所示,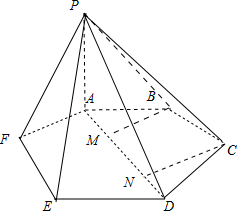 不妨设AB=2,则PA=4.
不妨设AB=2,则PA=4.
连接AD,作BM⊥AD,CN⊥AD,垂足分别为M、N,
由正六边形的性质可得,∠BAD=60°,∴AM=ABcos60°=1,同理DN=1,
四边形BCNM为矩形,∴MN=BC=2,∴AD=4.
∵PA⊥底面ABCD,∴PA⊥AD,∠PDA是直线PD与平面ABC所成的角.
在Rt△PAD中,tan∠PDA=
=
=1,∴∠PDA=
.
故答案为
.
 不妨设AB=2,则PA=4.
不妨设AB=2,则PA=4.连接AD,作BM⊥AD,CN⊥AD,垂足分别为M、N,
由正六边形的性质可得,∠BAD=60°,∴AM=ABcos60°=1,同理DN=1,
四边形BCNM为矩形,∴MN=BC=2,∴AD=4.
∵PA⊥底面ABCD,∴PA⊥AD,∠PDA是直线PD与平面ABC所成的角.
在Rt△PAD中,tan∠PDA=
| PA |
| AD |
| 4 |
| 4 |
| π |
| 4 |
故答案为
| π |
| 4 |
点评:熟练掌握正六边形的性质、线面垂直的性质和线面角的定义是解题的关键.

练习册系列答案
相关题目


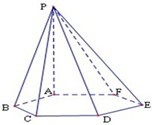 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论不正确的序号是
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论不正确的序号是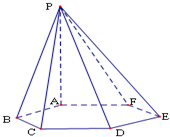 已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论不正确的是( )
已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论不正确的是( )