题目内容
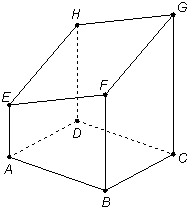（2008•深圳一模）如图是以正方形ABCD为底面的正四棱柱被一平面所截得的几何体，四边形EFGH为截面，且AB=AD=a，BF=DH=b．（Ⅰ）证明：截面四边形EFGH是菱形；
（Ⅱ）求三棱锥F-ABH的体积．
分析：（Ⅰ）证明截面四边形EFGH是平行四边形，然后证明对角线互相垂直即可证明截面四边形EFGH是菱形；
（Ⅱ）通过等体积法转化为VF-ABH=VH-ABF，求三棱锥F-ABH的体积．
（Ⅱ）通过等体积法转化为VF-ABH=VH-ABF，求三棱锥F-ABH的体积．
解答：解：（Ⅰ）证明：因为平面ABEF∥平面CDHG，且平面EFGH分别交平面ABFE、
平面CDHG于直线EF、GH，所以EF∥GH．
同理，FG∥EH．
因此，四边形EFGH为平行四边形．（1分）
因为BD⊥AC，而AC为EG在底面ABCD上的射影，所以EG⊥BD．
因为BF=DH，所以FH∥BD．
因此，FH⊥EG．（2分）
由（1）、（2）可知：四边形EFGH是菱形；
（Ⅱ）因为DA⊥平面ABFE，HD∥AE，所以H到平面ABF的距离为DA=a．
于是，由等体积法得所求体积VF-ABH=VH-ABF=
•S△ABF•DA=
×
ab×a=
a2b．
平面CDHG于直线EF、GH，所以EF∥GH．
同理，FG∥EH．
因此，四边形EFGH为平行四边形．（1分）
因为BD⊥AC，而AC为EG在底面ABCD上的射影，所以EG⊥BD．
因为BF=DH，所以FH∥BD．
因此，FH⊥EG．（2分）
由（1）、（2）可知：四边形EFGH是菱形；
（Ⅱ）因为DA⊥平面ABFE，HD∥AE，所以H到平面ABF的距离为DA=a．
于是，由等体积法得所求体积VF-ABH=VH-ABF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评：本题是中档题，考查直线与直线的垂直，四边形是菱形的证明方法，体积的求法，考查计算能力，转化思想．
练习册系列答案
相关题目
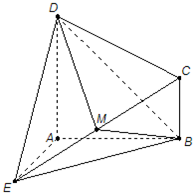（2008•深圳一模）如图所示的几何体ABCDE中，DA⊥平面EAB，CB∥DA，EA=DA=AB=2CB，EA⊥AB，M是EC的中点．