题目内容
曲线y=x2（x≥0），直线y=-3x+4及y轴围成图形的面积是（ ）
分析：求出两个曲线的交点坐标，利用积分的几何意义即可求区域面积．
解答：解：由
得x2=-3x+4，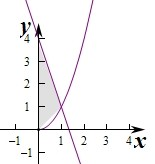
即x2+3x-4=0，解得x=1或x=-4（舍去），
∴根据积分的几何意义可知，对应的面积为S=
(-3x+4-x2)dx=（-
x2+4x-
x3）|
=-
+4-
=
．
故选：B．
|
即x2+3x-4=0，解得x=1或x=-4（舍去），
∴根据积分的几何意义可知，对应的面积为S=
| ∫ | 1 0 |
| 3 |
| 2 |
| 1 |
| 3 |
1 0 |
| 3 |
| 2 |
| 1 |
| 3 |
| 13 |
| 6 |
故选：B．
点评：本题主要考查积分的几何意义的应用，根据条件求出两曲线的交点坐标是解决本题的关键，要求熟练掌握常见函数的积分公式．
练习册系列答案
相关题目
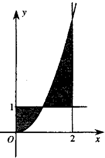如图，由曲线y=x2（x≥0）和直线x=0，x=2，y=1所围成的图形（阴影部分）的面积是
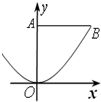（2013•怀化三模）如图，区域OAB由y轴，直线y=1及曲线y=x2（x≥0）围成，假设随机向该区域内投点，该点落在区域内每个位置是等可能的．现随机向区域投一点p，则直线OP的斜率小于1的概率是（ ）
（2009•大连二模）如图所示，若向圆x2+y2=2内随机投一点（该点落在圆x2+y2=2内任何一点是等可能的），则所投的点落在圆与y轴及曲线y=x2（x≥0）围成的阴影图形S内部的概率是（ ）