题目内容
已知圆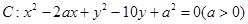 截直线
截直线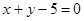 的弦长为
的弦长为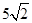 ;
;
(1)求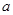 的值;
的值;
(2)求过点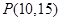 的圆的切线所在的直线方程.
的圆的切线所在的直线方程.
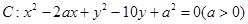 截直线
截直线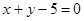 的弦长为
的弦长为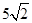 ;
;(1)求
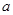 的值;
的值;(2)求过点
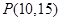 的圆的切线所在的直线方程.
的圆的切线所在的直线方程.(1)5(2) 或
或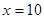
 或
或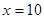
试题分析:(1)
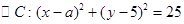 ,圆心
,圆心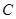 到直线
到直线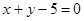 距离
距离 ,
,  ,
,
(2)若切线斜率不存在,
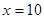 ,符合
,符合若切线斜率存在,设
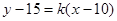 ,
,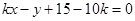

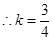
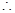 切线:
切线: 或
或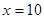
点评:关键是利用直线与圆的位置关系来求结合勾股定理,得到弦长,同时利用点斜式方程得到切线方程,属于基础题。

练习册系列答案
相关题目
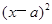 +
+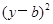 =
=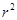 (ab≠0,r>0)的图像可能是
(ab≠0,r>0)的图像可能是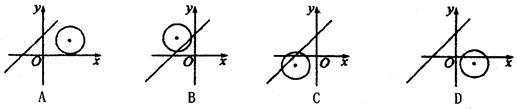
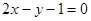 被圆
被圆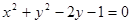 所截得的弦长.
所截得的弦长.  ,过点P的直线l与圆
,过点P的直线l与圆 相交于A、B两点,则
相交于A、B两点,则 的最小值为
的最小值为 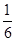 . B和C间的球面距离等于大圆周长的
. B和C间的球面距离等于大圆周长的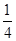 .如果球的半径是R,那么球心到截面ABC的距离等于( )
.如果球的半径是R,那么球心到截面ABC的距离等于( )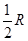 B.
B. 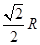 C.
C. 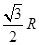 D.
D. 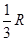
 所得的弦长为2,则直线的斜率为
所得的弦长为2,则直线的斜率为



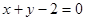 上的圆的方程是 .
上的圆的方程是 .