题目内容
点Q在x轴上,若存在过Q的直线交函数y=2x的图象于A,B两点,满足
=
,则称点Q为“Ω点”,那么下列结论中正确的是( )
| QA |
| AB |
分析:设Q(a,0),A(x1,2x1),B(x2,2x2),由
=
可得x2=2x1-a,2x2=2×2x1,得x1=a+1,x2=a+2,进而得到对于x轴上任意Q(a,0)点,总有A(a+1,2a+1),B(a+2,2a+2)满足题设要求.
| QA |
| AB |
解答:解:设Q(a,0),A(x1,2x1),B(x2,2x2),
所以
=(x1-a,2x1),
= (x2-x1,2x2-2x1).
因为
=
,
所以x2=2x1-a,2x2=2×2x1,得x1=a+1,x2=a+2.
即对于x轴上任意Q(a,0)点,总有A(a+1,2a+1),B(a+2,2a+2)满足题设要求.
故选B.
所以
| QA |
| AB |
因为
| QA |
| AB |
所以x2=2x1-a,2x2=2×2x1,得x1=a+1,x2=a+2.
即对于x轴上任意Q(a,0)点,总有A(a+1,2a+1),B(a+2,2a+2)满足题设要求.
故选B.
点评:解决此类问题的关键是熟练掌握向量的有关运算与指数函数的性质,考查学生的理解并且运用新知识的能力,此题属于中档题,属于新定义题时高考命题的热点之一.

练习册系列答案
相关题目
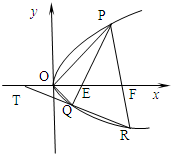 设P(x1,y1),Q(x2,y2) 是抛物线C:y2=2px(p>0)上相异两点,且
设P(x1,y1),Q(x2,y2) 是抛物线C:y2=2px(p>0)上相异两点,且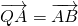 ,则称点Q为“Ω点”,那么下列结论中正确的是
,则称点Q为“Ω点”,那么下列结论中正确的是 ,则称点Q为“Ω点”,那么下列结论中正确的是( )
,则称点Q为“Ω点”,那么下列结论中正确的是( )