题目内容
设A为奇函数f(x)=x3+x+a(a为常数)图象上一点,在A处的切线平行于直线y=4x,则A点的坐标为 .
【答案】分析:由f(x)=x3+x+a是奇函数,知f(x)=x3+x,故f′(x)=3x2+1,设A(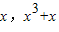 ),由函数f(x)=x3+x在A处的切线平行于直线y=4x,知
),由函数f(x)=x3+x在A处的切线平行于直线y=4x,知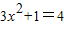 ,由此能求出A点的坐标.
,由此能求出A点的坐标.
解答:解:∵f(x)=x3+x+a是奇函数,∴a=0,即f(x)=x3+x,
∴f′(x)=3x2+1,
设A(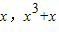 ),
),
∵函数f(x)=x3+x在A处的切线平行于直线y=4x,
∴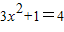 ,
,
解得x=±1,
∴A点的坐标为(1,2)或(-1,-2).
故答案为:(1,2)或(-1,-2).
点评:本题考查利用导数求曲线的切线方程,解题时要认真审题,仔细解答,注意合理地进行等价转化.
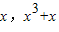 ),由函数f(x)=x3+x在A处的切线平行于直线y=4x,知
),由函数f(x)=x3+x在A处的切线平行于直线y=4x,知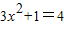 ,由此能求出A点的坐标.
,由此能求出A点的坐标.解答:解:∵f(x)=x3+x+a是奇函数,∴a=0,即f(x)=x3+x,
∴f′(x)=3x2+1,
设A(
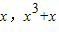 ),
),∵函数f(x)=x3+x在A处的切线平行于直线y=4x,
∴
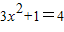 ,
,解得x=±1,
∴A点的坐标为(1,2)或(-1,-2).
故答案为:(1,2)或(-1,-2).
点评:本题考查利用导数求曲线的切线方程,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目