题目内容
三角形两边之差为2，夹角的余弦值为
，面积为14，那么，这个三角形的此两边长分别是（ ）
| 3 |
| 5 |
分析：利用平方关系即可得出sinB，再利用面积公式S△ABC=
acsinB，即可得出ac的值，与a-c=2联立即可得出a，c得值．
| 1 |
| 2 |
解答：解：如图所示，
假设已知a-c=2，cosB=
，S△ABC=14．
∵0＜B＜π，∴sinB=
=
．
又14=
acsinB，∴ac=35．
联立
，∵a，c＞0，解得
∴这个三角形的此两边长分别是5和7．
故选D．
假设已知a-c=2，cosB=
| 3 |
| 5 |
∵0＜B＜π，∴sinB=
| 1-cos2B |
| 4 |
| 5 |
又14=
| 1 |
| 2 |
联立
|
|
∴这个三角形的此两边长分别是5和7．
故选D．
点评：熟练掌握平方关系和面积公式S△ABC=
acsinB是解题的关键．
| 1 |
| 2 |
练习册系列答案
名校课堂系列答案
相关题目
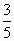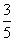，面积为14，那么这个三角形的此两边长分别是
，面积为14，那么这个三角形的此两边长分别是
，面积为14，那么，这个三角形的此两边长分别是（ ）
，面积为14，那么，这个三角形的此两边长分别是（ ）